



 |
 |
 |
 |
This page is still incomplete and, to use a term from the earlier days of the WWW: 'under construction'.
It is clear that the main unanswered question about the Voynich MS is: "what does it say?". At the same time one can ask: "why has nobody found the solution yet?". Does this mean that the MS could be meaningless after all? Or has someone already found the solution and we simply have not realised it? Or, alternatively, has everyone been looking in the wrong direction for the last 100 years? While that would seem unrealistic, the present page also addresses this question specifically.
On this page I already argued that at least the most common solution approach, namely finding a way to translate the text of the Voynich MS back to plain text, is fundamentally wrong. It could work, but only if several implied assumptions are all valid, most particularly that the MS includes a meaningful text in a language that we still understand. Now I have read and heard many times that, clearly, it wouldn't make sense for such a long MS to be meaningless so there has to be a possible translation. Even though that seems to make sense, still, it is again an assumption, and I dare say that a modern (21st Century) person may not be in the best position (1) to judge what would or would not make sense for someone creating a book 600 years ago.
Let me start by repeating a key phrase from this page:
We don't yet know whether the Voynich MS represents a meaningful text. What we do know for certain, however, is that some time in the past, somebody or some group of people sat down and wrote the Voynich MS using some method. [...] Unfortunately, we don't (yet) know this method. We can only imagine a multitude of different ways how it could have been created.
This text generation method is what we should be looking for, and in the following I will classify some high-level aspects of it using a tree structure. We will then see in which cases the usual 'decoding attempts' could be valid and in which cases they cannot lead to success.
At various points in the tree structure for the text generation method there are different options. All of these options are numbered. In the following I will avoid going into the question of the likelihood that one or the other option is correct. It is necessary to keep this completely open at this stage. It is in any case very hard to quantify in almost all cases. Instead, I will give what I call examples and challenges.
Examples are ways how a particular option could be explained, without aiming for completeness. They are just there to show that one should not discard any option off-hand.
Challenges are points that might not be easy to explain in case a particular option is chosen.
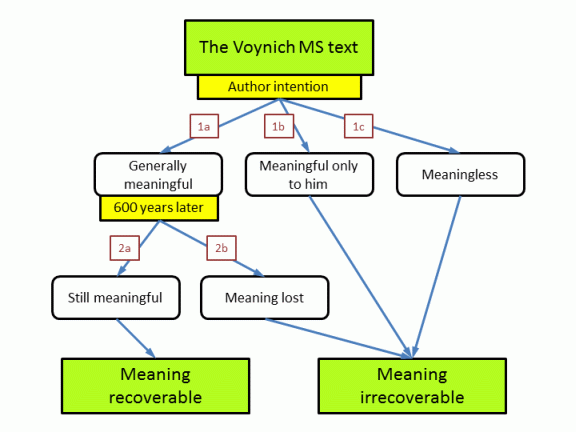
The total ensemble of all possible solutions is what I called the solution space in the previous page, and it is represented by the entire tree structure developed below. Please note that this tree is not intended to be the only possible way to analyse the problem. The questions about cipher vs. language, or what could be the plain text language are deliberately left out of this analysis. They will only start playing a role in case there is a meaningful plain text. The tree is developed primarily along the branch of meaningful solutions. The other branches are more difficult to develop.
Whether the text still has a recoverable meaning is addressed as a combination of two different questions. Question 1 is: what did the author intend 600 years ago. Question 2 is: in case he wrote something meaningful, can we still extract this meaning 600 years later?
Example(s):
This is the most easily understandable option, and the one that most people tend to assume automatically. The text would be written in any known language of the 15th Century, either well known or more exotic, and represented in a strange alphabet, possibly with some cryptography added as well.
Challenge(s):
There are two main problems that require an explanation in case this option is preferred. The first is how the word structure arises, and the second is why the solution has not yet been found by anyone.
Example(s):
To explain this option, let's just look at f116v of the Voynich MS. This has text written mostly in plain Roman characters. It is quite possible that this was written by the original MS composer/author. However, it has not been possible so far to make complete sense of it. Now what if the entire MS contains text similar to this? People decoding the text would not even recognise that they solved it, even if they did. Numerous other manuscripts exist that include some magical and nowadays basically meaningless text.
Challenge(s):
The main problem that requires an explanation in case this option is preferred is whether anyone could really write more than 200 pages in such a manner. How the word structure arises in this case would also require an explanation.
Example(s):
While the exact method given by Gordon Rugg does not work, the idea he proposes is a good example in general how this could be done with 15th Century means. The method proposed by Torsten Timm also fits into this category. Other methods could include generating / picking words from an existing text that has been written in a language or script unknown to the author.
Challenge(s):
One of the main problems that require an explanation in case this option is preferred is why the labels in the MS follow completely different word statistics than the main text. This cannot be the result of an arbitrary process.
This question relates to what the composer/author of the MS intended. Although the boundaries between the three proposed options may not be very precise, all possibilties can be associated to one of the three, even when it is a matter of taste. Anyone looking for a translation of the text should realise very clearly that he is choosing option 1a, and there are some points that require an explanation. Anyone proposing an alternative option similarly has some questions to answer.
This question further qualifies the case 1a above, that the original author intended to write something generally understandable. The question is whether this meaning is still recoverable now. Again, the boundary between 'yes' and 'no' may not be very precise.
Example(s):
Again, this is the most easily understandable option, and the one that most people tend to assume automatically. 'Recoverable' should be understood as 'in principle'. It should not necessarily be easy.
Challenge(s):
The main two challenges of option 1a are still valid: the first is how the word structure arises, and the second is why the solution has not yet been found by anyone.
Example(s):
The loss of the original meaning would happen, for example, in case a meaningful text has been encoded using an irreversible method. A variation of this is the so-called 'ignorant scribe' scenario, where a scribe unintentionally makes an inaccurate copy of the original, thereby eliminating critical information or introducing large errors. Another possibility for a loss of the original meaning is in case the original language is no longer known.
Challenge(s):
The main problem that requires an explanation in case this option is preferred is not a very strong one. It seems hard to imagine that the MS author or composer would make the mistake of using an irreversible method, and also the 'ignorant scribe' theory seems difficult to accept. A lost language is likely to still have cognates in modern times.
In the end we have two options: either there is a recoverable meaning or there is not. In the negative case, we have identified three high-level possibilities how this could have happened. Assuming that the MS has a meaning therefore implies that one assumes none of these three options applies.
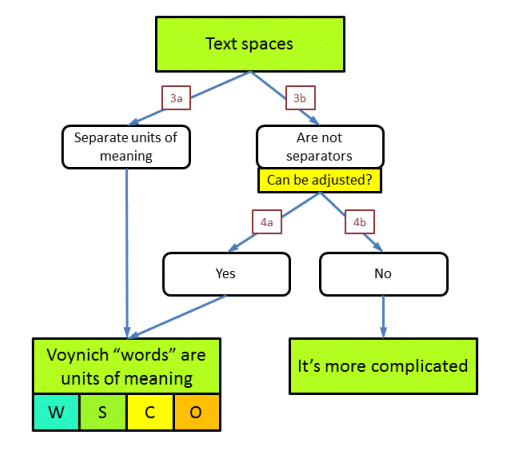
We are now ready to further explore the case where the MS text still has a recoverable meaning, and one of the first questions that arises is related to the spaces we see between groups of characters. In the analysis section we called these groups of characters 'word tokens'. Here, for brevity, I will just call them 'words'. The question is whether the spaces are really meant in the sense that these character groups indeed represent words, which is something that most people will almost automatically assume.
Also this question is addressed as a combination of two different questions. Question 3 is: are the word spaces as we see them real separators between units of information. Question 4 is: in case not, can we still (re-)introduce such spaces / separators in a (more-or-less) simple manner?
Example(s):
This is the most easily understandable option, and the one that many if not most people tend to assume.
Challenge(s):
The main two challenges of options 1a/2a are still valid: the first is how the word structure arises, and the second is why the solution has not yet been found by anyone.
Example(s):
In this case there are several possibilities. For example, it could be that some spaces are 'real' while others are dictated by orthography, as in the arabic script where there are breaks following characters that cannot be 'connected' to the next one. It should also be noted that many of the spaces in the MS are difficult to judge. They have highly variable width, leading to significant doubt in many places in the MS whether there is a space or not. Thus, the main two cases in this option are, on the one hand, that many or most of the spaces may be real but some may not be, or may be missing missing. In the other case, spaces could be completely arbitrary. Furthermore, the 'words' may not not represent complete words, but only parts of words (e.g. syllables) or even only single characters.
Challenge(s):
The main problem that requires an explanation in case this option is preferred is the observation that the label words in the MS, which are definitely single units, do occur most frequently in the running text separated by spaces
(2).
This is a very strong indication that the spaces do function as 'separators' of some sort.
The main purpose of this question is to make people realise that one should not necesarily assume that the 'words' in the MS really represent words in the way they are usually understood.
This question further qualifies the case 3b above, that the spaces we see in the Voynich MS are not (always) word separators.
Example(s):
This is only likely to be possible if some large part of the spaces we see in the MS is real. Another option would be that word spaces are to be ignored altogether, and another character is meant as a word separator.
Challenge(s):
There are several problems that would require an explanation in case this option is preferred. If a large fraction of the spaces are to be ignored because they are not real word spaces, this will have a negative impact on the word length distribution, as the average word length will increase significantly. In case word spaces are considered arbitrary, a reconstruction would be possible if another character should represent the word space. The big problem here is that no other charater is sufficiently frequent to take up this role. In general, this option would require a lengthy analysis and explanation.
Example(s):
This option just confirms the idea that word spaces are completely arbitrary, and it is not possible with easy means to identify the real ones.
Challenge(s):
The challenge for option 3b still applies here: it would need to be explained why or how the label words appear in the running text separated by spaces.
In the end we have two options: either we can identify the words in the text with 'units of meaning', or we cannot. Beside the examples given above, the negative case could also arise in very different scenarios (that have occasionally been proposed). These include suggestions that the text, as we see it, is not meaningful text but more like a 'background', against which we need to extract the real meaning from geometrical means, or by selecting individual characters using a grid, etc. etc.
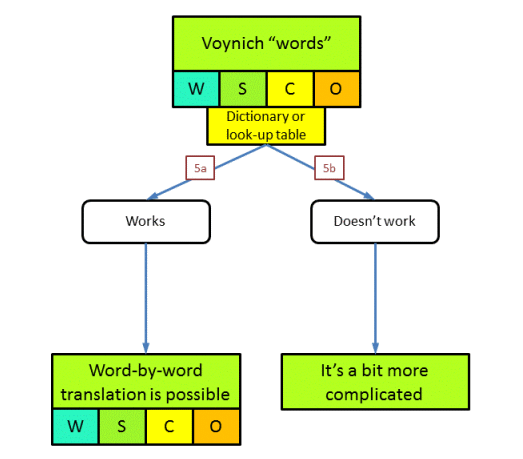
The units of meaning could represent (in the plain text) words, syllables, characters, or other, as indicated by the codes W, S, C, O in the above figure.
Having reached a point in the tree where the written words in the MS are representing units of meaning, the next logical question is, whether each word type we see in the MS is a consistent rendering of the same unit of meaning in the original or plain text. We need to keep in mind that we are looking at the process of writing the text by the author/scribe (whether translation or encryption or something else). The easiest case would be if one plain text word would be uniquely represented by one word in Voynichese, i.e. there is a one-to-one mapping. Another possibility would be that a plaintext word is represented by different Voynichese words (one-to-many). As long as each Voynichese word derives from only one original plain text word, we would still be able (in principle) to reverse this process and retrieve the plain text. A third possibility is a many-to-one mapping. Here, several different plain text words would map onto the same Voynichese word. This is in principle irreversible (3). Finally, many-to-many mappings could exist, which would equally be irreversible.
Example(s):
To deal with this question, we should imagine that there exists a 'dictonary' from plain text to Voynichese. It is not necessary that this dictionary physically exists. In the one-to-one mapping case, this dictionary has one entry for every plain text word, and it translates to one Voynichese word. If we had this dictionary, we could translate the text back. One possibilty is, of course, that this is how the MS text was written. The author created such a dictionary and used it. Another possibility is, that the plain text words were encrypted using a well-defined cipher that generates different cipher words for different plain text words. Finally, the text could be a rendition of an 'unusual' language in an invented alphabet, executed consistently.
The one-to-many mapping means that our (imaginary) dictionary has one entry for each plain text word, and this can translate to several different Voynichse words. If we had this dictionary, we could still translate the text back, assuming that there is no overlap in the Voynichese words from different plain text words. (In that case we should call it a many-to-many mapping). One possibility for ending up in such a situation is in case the author encrypted the text using a poly-aphabetic cipher, or added null characters.
Challenge(s):
A dictionary or look-up table to encrypt the MS text would not be a very practical manner. If it were a simple cipher, it is hard to understand why the MS text has not yet been deciphered. For a true one-to-many encoding, the word frequency distribution, which now follows Zipf's law, would be significantly disturbed.
One other challenge that exists in case this option is preferred is that we lack an explanation for the (relatively) many word repetitions, in particular also for the high-frequency words like daiin, and for the relative lack of repeating seqeunces.
Example(s):
This situation is a bit more difficult to imagine. It could be that the text is a very inaccurate rendering of an 'unusual' language, with loss of unique representation (several sounds mapping to the same character). It could also be that a cipher has been used that maps many to one. Finally, the text could include a great number of mistakes. In these cases, we are basically in the situation of option 2b above: meaning has been lost. This depends on the level or amount of redundancy that has been created.
Challenge(s):
It is also not easy to come up with challenges for this option. It remains to be seen whether the Zipf law would still be followed by a text that was generated using a many-to-one or many-to-many mapping, but it remains entirely possible.
At the end of this question we end up with basically two options. Either the text that we have in the Voynich MS could be translated back to a plain text using a consistent word-for-word substitution, or it cannot. Again, my feeling is that people naturally tend to assume the former, but the present analysis should show that this involves a number of unconscious assumptions.
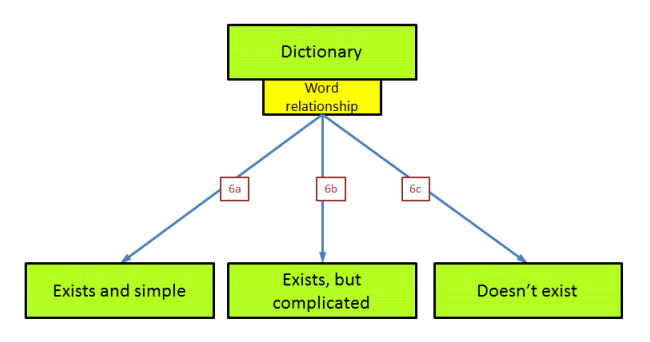
We have now reached the point where there exists (in theory) a dictionary that would allow a word for word translation of a plain text into Voynichese and vice versa. We may compare the plain text words and the Voynichese words, and see if there is any relationship between the two. There are various possibilities. Such a relationship may exist and be straightworward, it may exist and be more complicated, or it may in fact not exist. These three options are now compared.
Example(s):
This is again very easy to imagine, for example if the plain text is a language which is simply rendered by an invented alphabet, or in case it was a written text that had been encrypted using a very simple cipher, such as a simple substitution. In such a case, the dictionary would not be needed, but one would just have to remember the 'rule' to convert one to the other.
Challenge(s):
While this option is automatically assumed by most newcomers to the MS, the big problem is that in this case the solution should have long been found. The character entropy values of the Voynich MS text also preclude that the text is one of the well known languages just converted by simple substitution.
Example(s):
This is a variety of the first option, and it would still have allowed the author to create the text without actually consulting a long dictionary. It is hard to come up with good examples for the precise form of this relationship. It could be a moderately complicated cipher, or some as yet unforeseen way to turn plain text into Voynichese.
Challenge(s):
It is equally hard to come up with specific difficulties related to this option. It seems one way in which the problem could have remained unsolved for such a long time. A very complicated cipher would be anachronistic, though.
Example(s):
In this case, the plain text words would indeed have been written in a dictionary, or rather a code book, with in principle arbitrary entries for the resulting 'code'. This is one way in which the word pattern would not be a big problem, since this could have been part of the design. The 'code' could even have been generated in the form of a number system, although such a system has not been identified so far, and there are many exceptions to the word pattern.
Challenge(s):
The obvious problem in case this option is selected is that it would have been quite inconvenient to generate the text in this manner, unless the author had a remarkable memory. In practice, it would have required the author to look up (almost) every word before writing it down. This would have been in a draft, to be copied as a fair copy later.
These three options are not fundamentally different, but one or two of them would have been far more practical to implement than the third. All three only play a role in case a word by word translation of the text is possible, which is far from certain.
Taking all questions and options together, we may draw a simplified version of the tree structure as shown below. In this tree, I have split the entire 'solution space' into two parts. The part A (in green) concerns the case where the text has a meaning, and a word by word translation of the text is possible. Part B (in red) concerns all other cases.
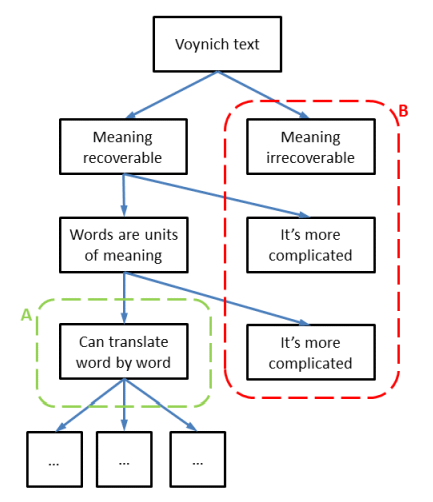
It is now possible, for any proposed solution, to identify the 'box' or the category into which it falls. As an example, the solution of Newbold is one where the text is meaningful (branch 1a), the meaning is still recoverable after 600 years, at least according to him (branch 2a), but words are not units of meaning (branch 3b and 4b), since he reads the text from the fragmented edges of the characters.
Another use of this tree structure is the demonstration that anyone who starts working on a 'solution' of the MS, by substituting Voynich characters into plain text letters in some language, is immediately jumping into the lower left box above (under the green A boundary), meaning that a whole array of hidden or subconscious descisions has been made.
Finally, one may wonder what is the likelihood that the 'truth' is in part A or in part B. This question cannot be answered, except that neither of the two probabilities are zero. I believe that the main 'divider' is the question whether the words in the MS are units of meaning. Analysing the words (both the word types and their frequency) should be able to tell us if they are, or are not, units of meaning.
 |
 |
 |
 |