



 |
 |
 |
 |
This page still requires more work, and should also be further extended.
This page can be considered a continuation of a preceding page that looked into the detailed character frequency distribution and the resulting anomalous entropy of the Voynich MS text. It is necessary to have read that page, before going through the present page.
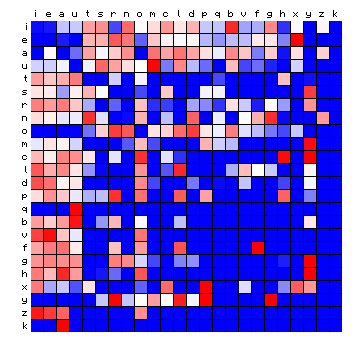
Figure 1 below is a copy of Figure 10 of this preceding page. It shows the difference between the character pair distributions of a known plain text in Latin and the FSG transliteration of the Voynich MS.
| Mattioli, Latin | Voynich MS, FSG |
|---|---|
 |
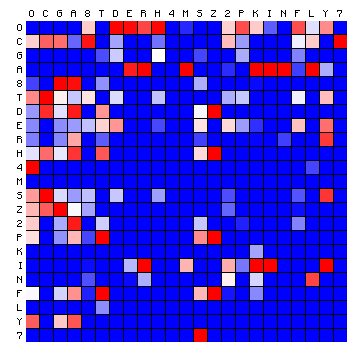 |
Figure 1: relative character pair distributions of Latin and Voynich text (FSG) compared
The figure for the Latin plain text is dominated by the alternation of vowels and consonants, and the fact that such combinations are the ones that tend to have the highest frequencies. In the preceding page, this was true for all four plain texts used, though the figure for the German text "Tristan" looked somewhat different from the other three. This is presumably because there are more consonants among the highest-frequency characters.
It is of interest to redo these plots by separating the vowels from the consonants. For the known languages this could be done easily, but for the text of the Voynich MS we do not know which characters are vowels and which are consonants, or in fact if the characters in the Voynich MS alphabet can really be separated in this way.
This problem can be approached by applying a two-state Hidden Markov Model (HMM) to all texts. This technique has been introduced already with a short dedicated description. For texts in most common languages this tends to classify all characters into vowels and consonants, though sometimes with some minor 'surprises'.
I am in the process of doing this analysis based on my own, alternative implementation of an HMM algorithm, which is explained in more detail on a dedicated page.
For texts in known languages the tool converges fairly quickly and produces very similar results to the standard implementation, for those cases in which it has been compared. For the text of the Voynich MS the results reported by Reddy and Knight (2011) (1) suggest that this method is not successful in identifying vowels and consonants in the Voynich MS text (2).
One important difference between my alternative implementation and the traditional Baum-Welch approach is that it is possible to treat spaces as a separate, third state (3). This feature, which is logical from a character-statistics point of view, helps considerably in the convergence. In all of the following experiments, this feature is used, as indicated by the "+" sign following the number of states for each case.
In the entropy calculations presented at this web site in general, and on a previous page in particular, the space character was left outside consideration. Consequently, it was not represented in any of the graphs. In the present page, the space character plays a more important role.
The results of all on-going experimentation are shown in the following. The first plot shows the expected effect on the organisation and colour distributions in these plots.
Figure 2: expected patterns of vowel and consonant frequency distributions
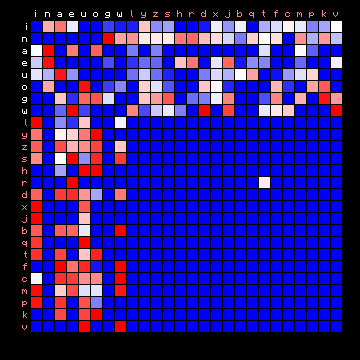
The following sets of figures show the effect of the sorting by Hidden Markov states on the Mattioli text. Figure 3 shows the characters sorted by decreasing frequency. This figure is very similar to Figure 7 of the preceding page. The only difference is that the space character is included as well, as the first character on both vertical and horizontal scales. This will be done for all following plots on this page (work in progress).
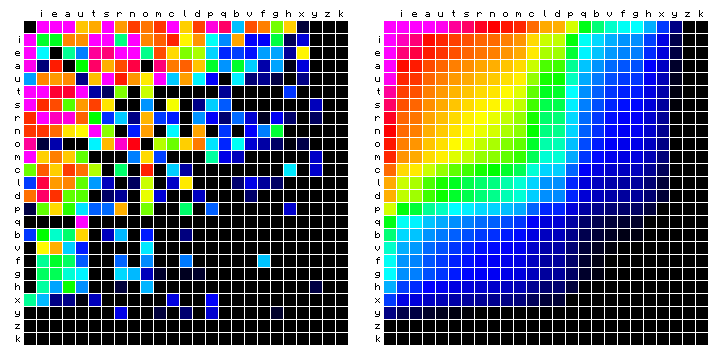
Figure 3: Mattioli, by character frequency
Figure 4 shows the same statistics sorted in a different way. First are all vowels in decreasing frequency, followed by all 'consonants' in decreasing frequency. Effectively, it turns out that the 'vowel' state tends to include the most frequent non-space character. The characters in the legend have been colour-coded to show the different states.

Figure 4: Mattioli, HMM-sorted
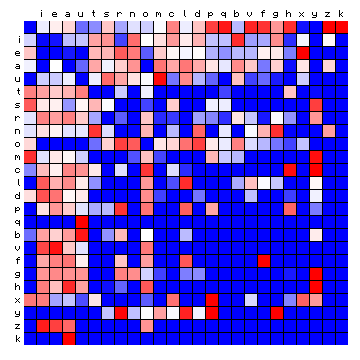
Figure 5 shows the effect of the sorting in side-by-side plots of the relative frequencies. For the meaning of this, see the preceding page.
| Mattioli, by frequency | Mattioli, HMM-sorted |
|---|---|
 |
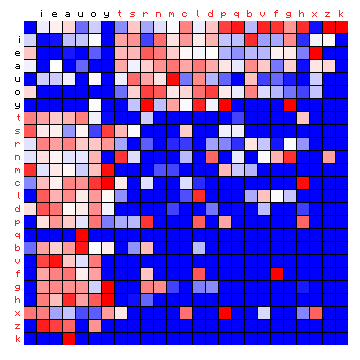 |
Figure 5: effect of vowel/consonant separation (by HMM) on Mattioli text (Latin)
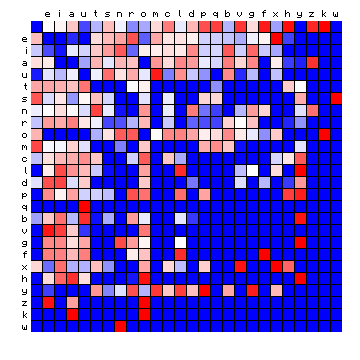
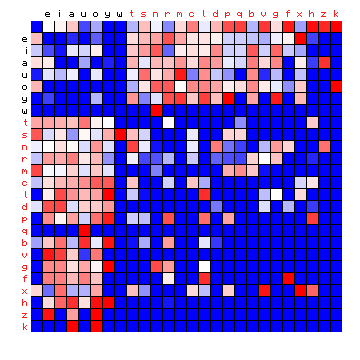
The same exercise can be performed on the other three plain texts, and this is shown in the following:
| Pliny (Latin), by freq. | Pliny (Latin), HMM-sorted |
|---|---|
 |
 |
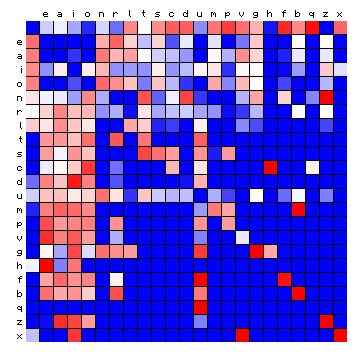
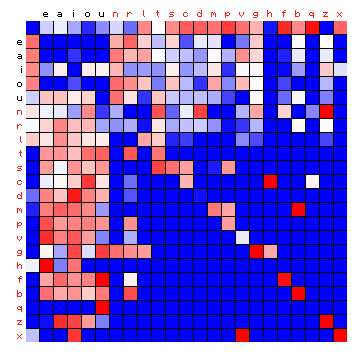
| Dante (Italian), by freq. | Dante (Italian), HMM-sorted |
 |
 |
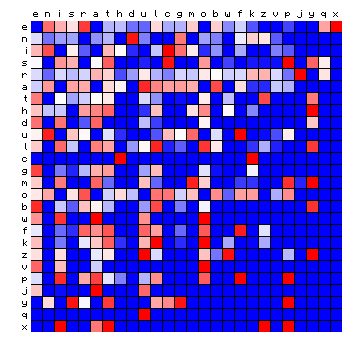
| Tristan (German), by freq. | Tristan (German), HMM-sorted |
 |
 |
Figure 6: effect of vowel/consonant separation (by HMM) on other texts
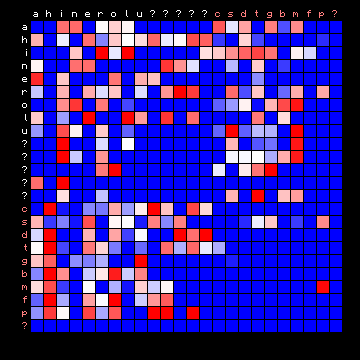
The separations largely confirm the expected split into vowels and consonants, with a few cases where an individual character appears 'on the wrong side'. For Italian the effect is only minor, since the four main vowels are also the four most frequent characters. Before summarising this, it is of interest to repeat the experiment by using three states instead of two (again with an additional space-only state). The results are shown below.
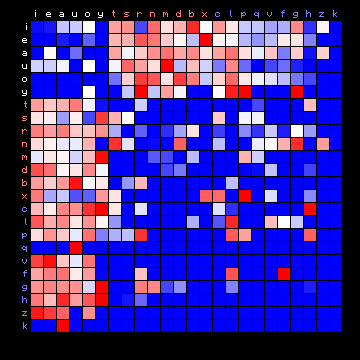
| Mattioli (Latin), 2+ states | Mattioli (Latin), 3+ states |
|---|---|
 |
 |
| Pliny (Latin), 2+ states | Pliny (Latin), 3+ states |
 |
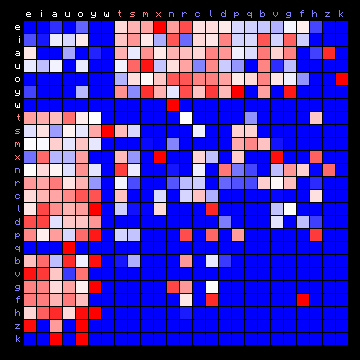 |
| Dante (Italian), 2+ states | Dante (Italian), 3+ states |
 |
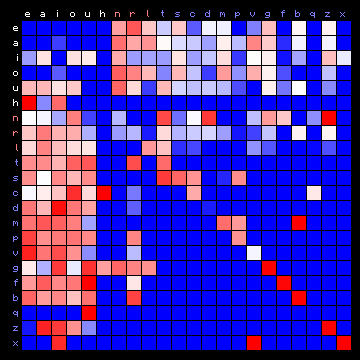 |
| Tristan (German), 2+ states | Tristan (German), 3+ states |
 |
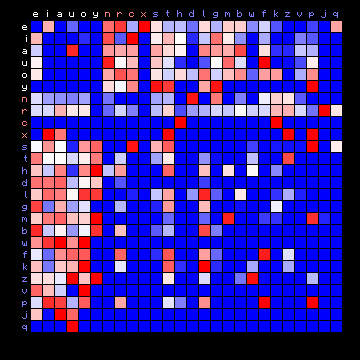 |
Figure 7: 2+ state and 3+ state HMM results for all plain texts
In these cases the vowels all tend to appear in one state, and the consonants are separated into two different states.
The success of the analysis can be measured by the statistical difference between the actual character transition probabilities and the simulated value based on the Markov process output (computed as Bhattacharyya distance). These statistics are shown below. The absolute values have no clear meaning, but the relative values clearly show the level of success of each process. The a priori values reflect the case that all characters are equally likely to be emitted by each of the states.
| Text | A priori | 2+ states | 3+ states |
|---|---|---|---|
| Mattioli | 0.157 | 0.093 | 0.083 |
| Pliny | 0.140 | 0.086 | 0.079 |
| Dante | 0.178 | 0.104 | 0.091 |
| Tristan | 0.162 | 0.136 | 0.113 |
Table 1: measure of "fit" for 2+ state and 3+ state HMM results for all plain texts
For Latin and Italian there is only a minor improvement in the statistics when going from 2+ states to 3+ states. For Italian it has the side effect of moving the character 'h' from the consonants group to the vowels group. As one can see in the figures for the Italian text, one of the primary uses of 'h' is in the combinations 'ch' and 'gh', and is a modifier to change the sound of the 'c' and 'g' consonants, always before 'e' or 'i'. In this function, it is neither a consonant nor a vowel. Another use is as a mute consonant, mostly at the beginning of words.
For the German text the value for the 3+ state solution is clearly better than the 2+ state solution. Also, the frequent character 'c' is moved from the vowels state to one of the consonant states. The following table summarises the results of the separation of characters following the 3+ state result.
| Mattioli (Latin) |
"Vowels" | i e a u o y |
|---|---|---|
| "Consonants" group 1 | t s r n m d b x | |
| "Consonants" group 2 | c l p q v f g h z k | |
| Pliny (Latin) |
"Vowels" | e i a u o y w |
| "Consonants" group 1 | t s m x | |
| "Consonants" group 2 | n r c l d p q b v g f h z k | |
| Dante (Italian) |
"Vowels" | e a i o u h |
| "Consonants" group 1 | n r l | |
| "Consonants" group 2 | t s c d m p v g f b q z x | |
| Tristan (German) |
"Vowels" | e i a u o y |
| "Consonants" group 1 | n r c x | |
| "Consonants" group 2 | s t h d l g m b w f z v p j q |
Table 2: result of vowel and consonant separation for the four plain texts using HMM
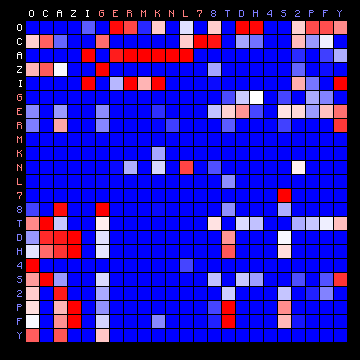
We may now look at the results for the Voynich MS text. Initially, this is done for the three cases FSG, ZL and ZL (Cuva), which have an alphabet size similar to the used plain texts. From the beginning, both 2+ state and 3+ state solutions are analysed. Since the most frequent character in the languages of the four plain texts is a vowel, for the Voynich MS text by convention we will call the 'vowel' state the one that includes the single most frequent character. For all available transliterations this is the character o. The results are show below.
| FSG, 2+ states | FSG, 3+ states |
|---|---|
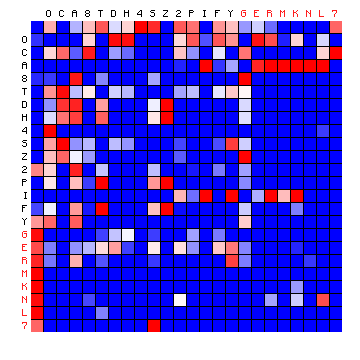 |
 |
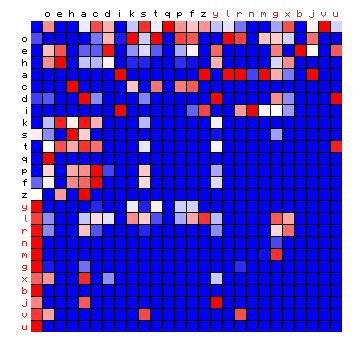
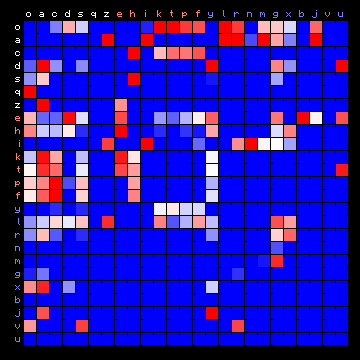
| ZL (Eva), 2+ states | ZL (Eva), 3+ states |
 |
 |
| ZL (Cuva), 2+ states | ZL (Cuva), 3+ states |
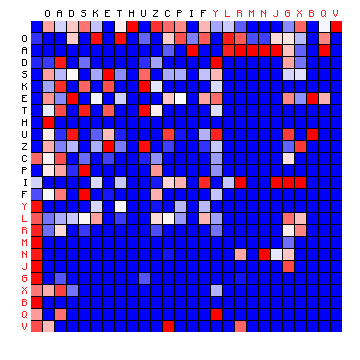 |
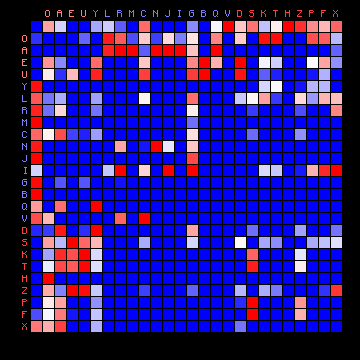 |
Figure 8: 2+ state and 3+ state HMM results for three of the Voynich MS transliterations.
It was pointed out that the "vowel" state should include the most frequent character, but for all cases of a 2-state HMM the vowel state includes more than half the character set, which is not to be expected. On the other hand, the three-state solutions show a grouping of characters into states that is more or less similar to the plain text cases. Still, the appearance of the plots is very different from that of the plain texts.
Also for the Voynich texts, the "measure of fit" for each of the experiments has been computed (similar to Table 1 above). The result is shown below.
| Text | A priori | 2+ states | 3+ states |
|---|---|---|---|
| FSG | 0.326 | 0.225 | 0.189 |
| ZL (Eva) | 0.396 | 0.307 | 0.280 |
| ZL (Cuva) | 0.314 | 0.222 | 0.185 |
Table 3: measure of "fit" for 2+ state and 3+ state HMM results for the Voynich MS transliterations
One may observe that all values are much higher than those of the plain texts.
Finally, the following table shows the results of the separation of characters of the Voynich texts, according to the 3-state HMM analysis.
| Voynich (FSG) |
"Vowels" | O C A Z I |
|---|---|---|
| . | ||
| "Consonants" Group 1 |
G E R M K N L 7 | |
| | ||
| "Consonants" Group 2 |
8 T D H 4 S 2 P F 0 Y | |
| | ||
| Voynich (ZL - Eva) |
"Vowels" | o a c d s q z |
| | ||
| "Consonants" Group 1 |
e h i k t p f | |
| | ||
| "Consonants" Group 2 |
y l r n m g x b j v u | |
| | ||
| Voynich (ZL - Cuva) |
"Vowels" | O A E U |
| | ||
| "Consonants" Group 1 |
Y L R M C N J I G B Q V | |
| | ||
| "Consonants" Group 2 |
D S K T H Z P F X | |
| |
Table 4: result of character separation into 2 or 3 states, for the Voynich MS transliterations
From earlier experimentation with vowel-consonant separation, e.g. using Sukhotin's algorithm
(4),
the following characters have typically been identified tentatively with vowels:
.
In the above cases, the main difference is that tends to be grouped with the "consonants".
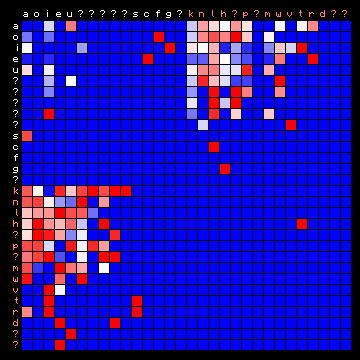
Following up from a comment at the end of the preceding page, we may now also look at some less standard languages that are known to have a low bigram entropy. The corresponding 2+ state results are shown below. Again, non-Ascii characters (e.g. characters with diacritics) cannot be rendered by the used font, and are replaced by a question mark (?).
| Minjiang (Chinese) | Scottish (Gaelic) |
|---|---|
 |
 |
| Hawaiian | Tagalog (Philippines) |
 |
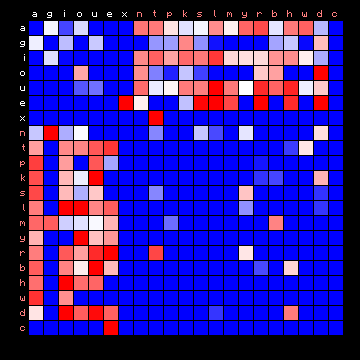 |
| Voynich (FSG) | Voynich (ZL - Cuva) |
 |
 |
Figure 9: 2+ state HMM separation for four 'exotic' languages.
Again, the plain texts show a much clearer separation into vowels and consonants than the Voynich MS text. The possible exception is Scottish Gaelic, and here also a 3+ state solution may be attempted:
| Voynich ZL (Cuva) | Scottish (Gaelic) |
|---|---|
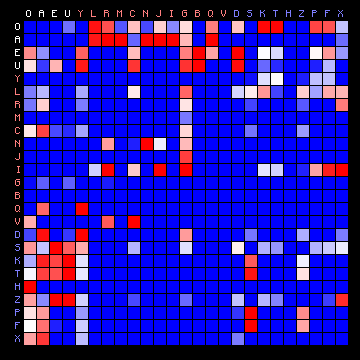 |
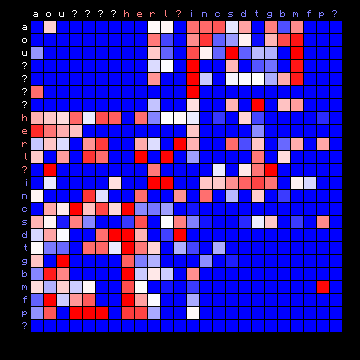 |
Figure 10: 3+ state HMM separation for Scottish Gaelic.
While the difference is not as great as with all other cases, still the Voynich text has more 'empty areas' than the Scottish plain text.
It is of interest to compare the actual character distributions of one case (ZL Cuva, 3+ states) with the simulated distribution. This simulated distribution describes a simulated text that would be output by a Hidden Markov chain with the A and B matrices that were optimised from the ZL Cuva text, for three+ states. This is shown in Figure 11 below. The meaning of this figure is explained more fully in the page describing the method. It is especially interesting to include the space character in these figures.
| ZL (Cuva) REAL, 3+ states | ZL (Cuva) SIMULATED, 3+ states |
|---|---|
 |
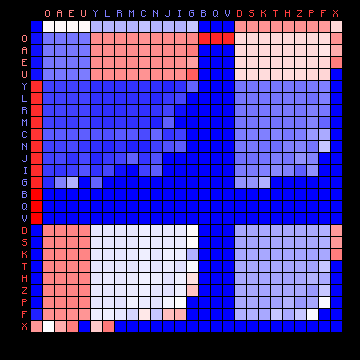 |
Figure 11: 3+ state HMM results for the Voynich MS transliteration using "Cuva". Left: actual transition frequencies. Right: transition frequencies for the HMM-generated text.
A first comment concerns the three bright red squares in the right-hand plot in the columns B, Q and V. These are very rare characters and the colour of the squares is an artefact that should be ignored. The same is true for the rows B, Q and V.
The simulated plot is clearly not at all symmetric. Instead, it shows a clear preferences for individual states to be followed by specific other states. Keeping in mind that the first character of each pair is on the vertical scale, and the second character on the horizontal scale, we may observe that:
This means that characters prefer to follow each other according to their states, as follows:
space -> state 3 -> state 1 -> state 2 -> space
This interesting result confirms the observations made in the past by Jim Reeds and by Reddy and Knight, as mentioned in the introduction.
The above results shows the difference between the Voynich MS text and that of a number of plain texts even more clearly than the previous page related to entropy.
 |
 |
 |
 |