



 |
 |
 |
 |
An earlier version of this page included a discussion of Hidden Markov Modelling. This has been moved to a dedicated page, which is still under work.
The topic of text entropy, its meaning and how it can be estimated for a given text has been introduced here. In general, the entropy is a single value computed from a frequency or probability distribution. Clearly, each frequency distribution will have its corresponding entropy value, but any particular entropy value can match an infinite number of different distributions. The entropy value is maximum in case all frequencies are equal, and is smaller in case this distribution is skewed.
All analyses that are presented here are based on counts of characters. This means that we are tacitly equating probability with frequency, while strictly speaking the frequency is an estimate of the probability.
The first order entropy, or single character entropy, is computed from the distribution of character frequencies in a text. The second order, or character pair entropy is computed from the distribution of character pairs.
If the text were an arbitrary sequence of characters with a given single-character frequency distribution, then, in each character pair, there would be no dependency between the first and second character. The second, or following character does not depend on the previous character. In this case the character pair entropy value is twice that of the single character entropy. In reality, this is not the case. We will come back to this further below.
One of the choices to be made is how to treat word spaces (effectively space characters). One can either count them among the set of characters, or not. In case one does not, one also limits the character pairs to be analysed to those 'within words'.
From the definition (i.e. the formula) of entropy, it is immediately obvious that the entropy values do not change if a piece of text is encoded using a simple substitution code. If characters are consistently replaced by others, the counts, and therefore the list of frequencies is not changed. This will not be true for other types of substitution codes (one-to-many, many-to-one or many-to-many).
In case the Voynich MS were a simple substitution cipher of a meaningful plain text in some known language, then the character counts (and therefore the entropy) would be similar to other texts in the same language. This is what Bennett looked at (1), and he found that the entropy values of the Voynich MS text were considerably lower than that of most comparison texts in known languages that he used. We will do the same here, but not only look at the entropy values, but also at the detailed distributions.
The following character distributions have been computed for the Voynich MS text from existing, large transliteration files. The alphabets used, and the source of the files, has been explained on this page. The files have been pre-processed (2), in order to remove illegible characters and characters that are not standard ASCII. The numbers on the vertical scale are counts. Since we do not know the sorting order of the characters, initially they are listed by decreasing frequency.
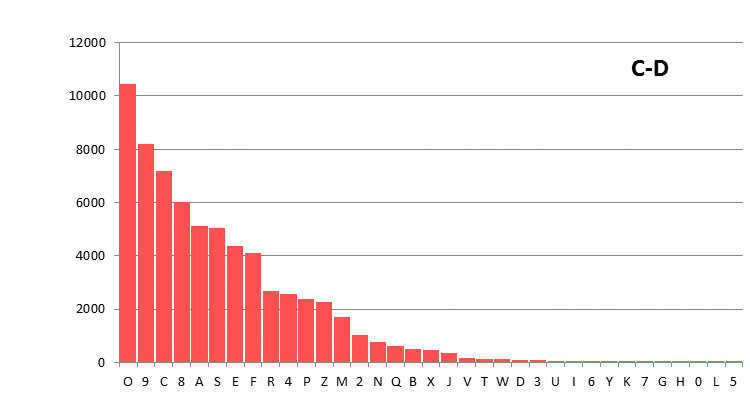
Figure 1: The Currier-D'Imperio transliteration, using the Currier alphabet.
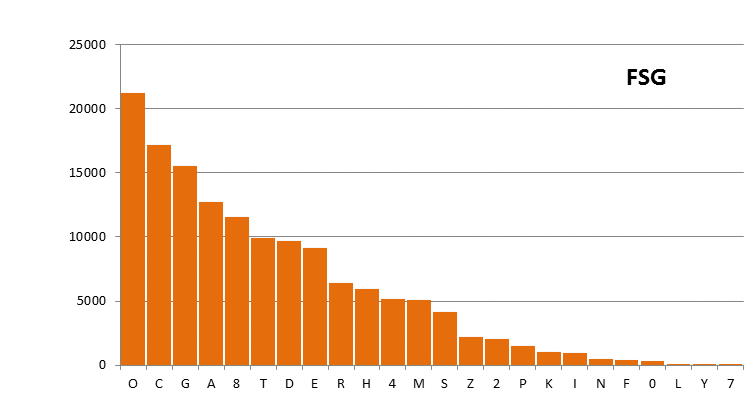
Figure 2: the FSG transliteration, using the FSG alphabet.
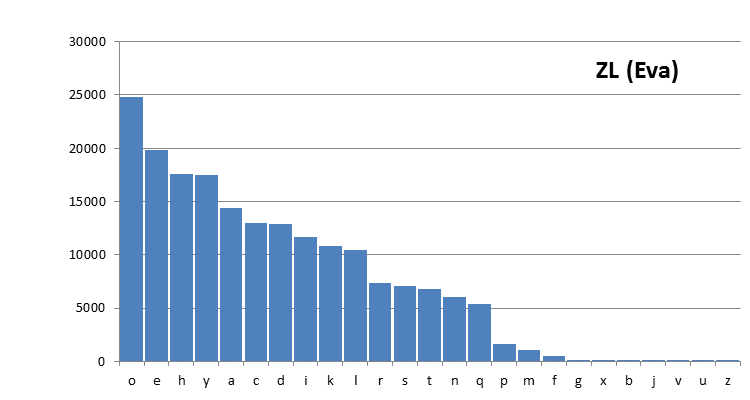
Figure 3: the Zandbergen-Landini transliteration, using the Eva alphabet.
In the following figure, the same transliteration has been converted to the Cuva alphabet (which has been defined here):
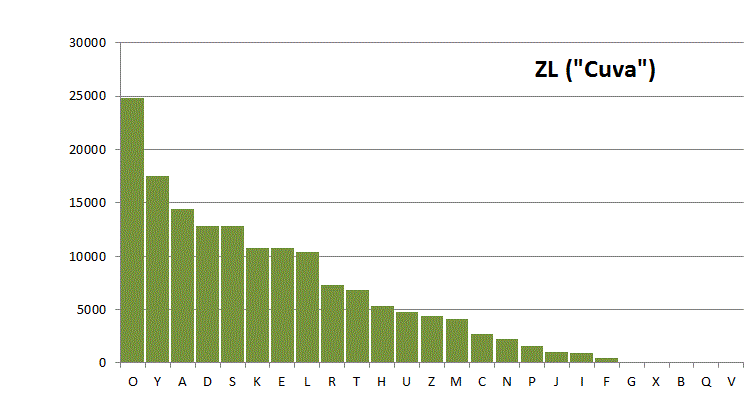
Figure 4: the same (ZL) transliteration using the Cuva alphabet.
Differences between these plots are due to the different definitions of the alphabets, and to some extent also to the different scope of the files. That second point mainly affects the C-D transliteration file, which is only half the size of the others.
These plots may be compared to one for a known plain text. Many such texts have been analysed, and below I include one example, from the first 120,000 characters of the Latin edition of Dioscurides by Mattioli, which was written in the middle of the 16th century (3). Also this text, and all further plain texts used in this page, have been pre-processed in order to:
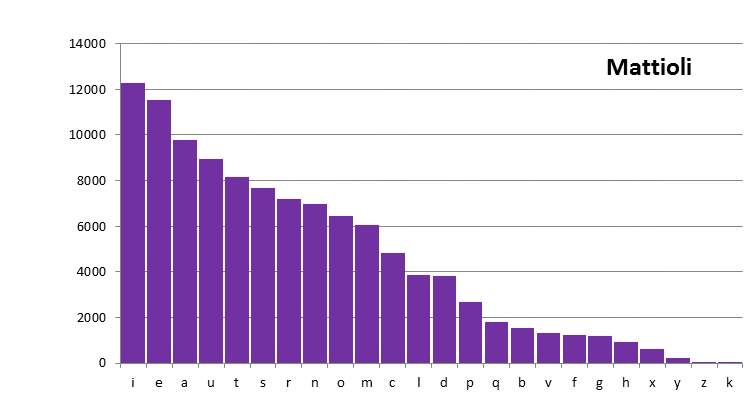
Figure 5: the Latin text of Mattioli
It is hard to draw any firm conclusions from a visual comparison of these plots. The frequency distribution of the Latin texts appears to decrease a bit more gradually than those of the Voynich MS transliterations, but this is a qualitative impression.
The following table lists the single character entropy values for the four different Voynich MS transliterations, and for four plain texts. In these figures, spaces have not been counted as characters. Apart from the single character entropy values for all characters, it also lists the character entropies for the first characters of words and the last characters of words.
| Text | Language | Nr. of chars. | Character entropy |
First char. entropy |
Last char. entropy |
|---|---|---|---|---|---|
| Voynich MS (part) | C-D transcr. | 66,587 | 3.857 | 3.437 | 2.689 |
| Voynich MS | FSG transcr. | 142,770 | 3.829 | 3.382 | 2.557 |
| Voynich MS | ZL transcr. (Eva) | 188,862 | 3.862 | 3.206 | 2.541 |
| Voynich MS | ZL transcr. (Cuva) | 156,414 | 3.872 | 3.369 | 2.686 |
| Mattioli | Latin (16th cent) | 108,960 | 4.036 | 4.122 | 3.355 |
| Pliny | Latin (classical) | 101,169 | 3.998 | 4.073 | 3.380 |
| Dante | Italian (14th cent) | 130,142 | 4.014 | 4.033 | 2.941 |
| Tristan | German (modern) (4) | 75,473 | 4.022 | 4.126 | 3.295 |
Table 1: single character entropy of some plain text in three languages,
and of various transliterations of the Voynich MS text.
The single character entropy of the Voynich text is consistently lower than that of the source texts, by a relatively small margin. The four Voynich transliterations have a mean entropy of 3.829 ± 0.044 and the four plain texts have 4.014 ± 0.016. The difference between the two averages is 0.189, which is still significantly greater than the variation in either value.
A clearer picture emerges from the statistics of the first and last characters of the words. For the four plain texts, the first characters have almost identical entropies as the set of all characters. The word final characters have a much reduced entropy value. This is most conspicuous for the Italian text. For the Voynich text we see that, in addition, word initial characters have a significantly reduced entropy, while the reduction for the word final characters is even more pronounced. This is illustrated by Figure 6 below, where the entropy of the word-initial characters is on the horizontal scale, and the word-final characters on the vertical scale.
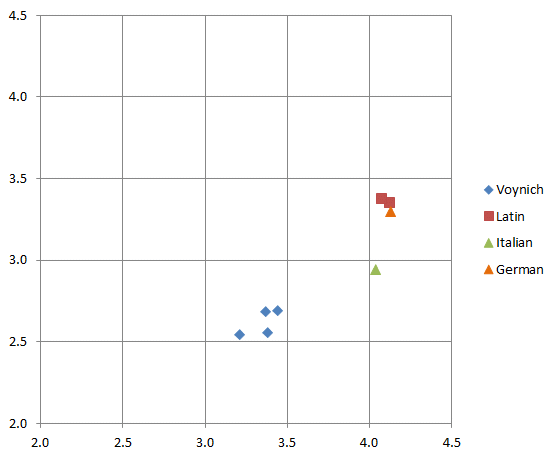
Figure 6: character entropies of first characters (horizontal) and last characters (vertical) of words
As already shown by Bennett and others (5), it is especially for character pairs that the entropy values of the Voynich MS text are anomalous. We shall see below that this is not just a matter of a lower entropy value, but the entire character pair frequency distribution is unusual.
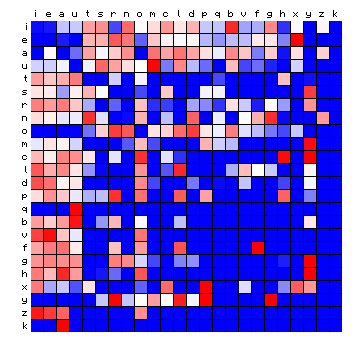
Let us start by visualising the character pair frequency distribution of the Latin text of Mattioli, again not counting word spaces. In the following plots, the first character is on the vertical scale (in decreasing frequency from top to bottom), and the second character on the horizontal scale (in decreasing frequency from left to right). The order of the characters is the same as in Figure 5 (the plot labelled "Mattioli") above. In the first Figure (Figure 7 below), the left-hand square shows the actual distribution of character pair frequencies. The right-hand square shows what the pair frequencies would have been, if there was no dependency between the two characters (6). The difference clearly shows the preference of certain characters to combine with others.
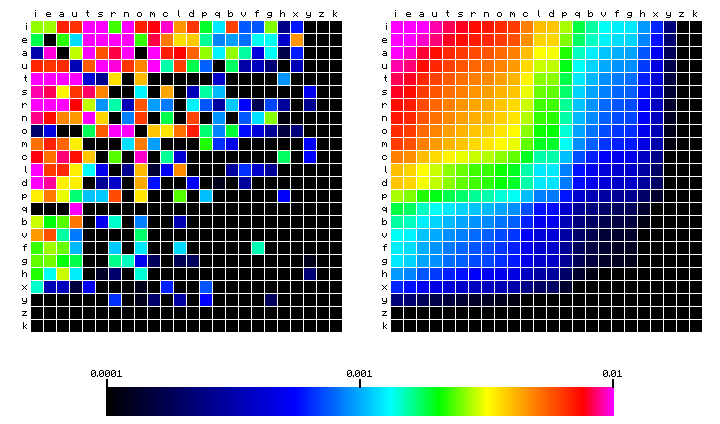
Figure 7: character pair frequency distribution for the Mattioli text (Latin)
To visualise the difference, we may also plot the ratio of the left and right figures. This is shown below. Red colours mean a preference or "over-representation" of certain pairs, while blue means an "under-representation".
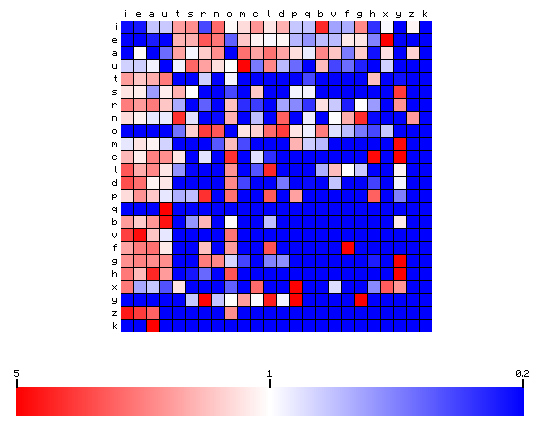
Figure 8: relative character pair frequency distribution for the Mattioli text (Latin)
We may now draw the same plots for other texts. The following is for the FSG transliteration of the Voynich MS. It uses the same colour scale, which is not repeated.
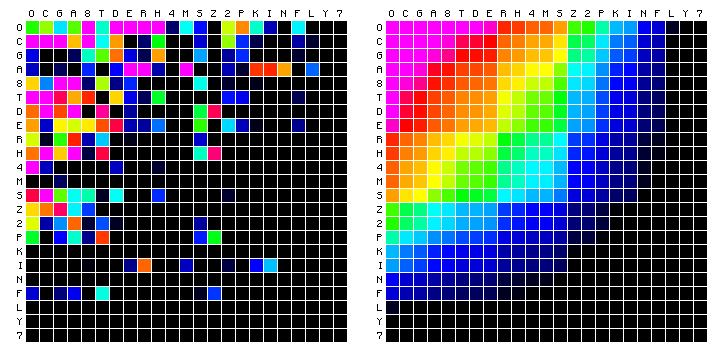
Figure 9: character pair frequency distribution for the Voynich MS text (FSG)
We see immediately that there is a very different pattern. The difference may be characterised by two aspects:
At this point we may come back to an observation about the behaviour of entropy in relation with simple substitution ciphers. In the above plots, the squares have been sorted from high to low frequency. These plots would remain completely unmodified if the text was passed through a simple substitution cipher. The only thing that would change would be the text symbols written near each row and column.
Thus, if the text of Mattioli were encrypted by a simple substitution, this text would immediately become illegible, but the character pair plot as shown on this page would look identical to the one for the plain text (apart from the character labels).
This clearly demonstrates that it is not possible to apply a simple substitution to the FSG transliteration of the Voynich MS text, and come up with meaningful Latin. Many character combinations will be missing. To visualise this, the following figure presents the two plots of the ratios, where the one for Latin and for the Voynich MS text (in FSG) are shown side by side.
| Mattioli, Latin | Voynich MS, FSG |
|---|---|
 |
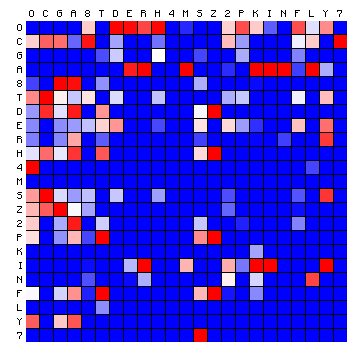 |
Figure 10: relative character pair distributions of Latin and Voynich text (FSG) compared
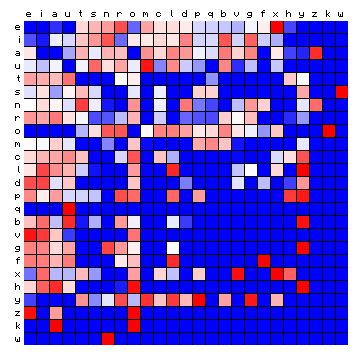
Similar plots have been made for other plain texts and for the other Voynich MS transcriptions, which are shown below.
| Mattioli (Latin) | Pliny (Latin) |
|---|---|
 |
 |
| Dante (Italian) | Tristan (German) |
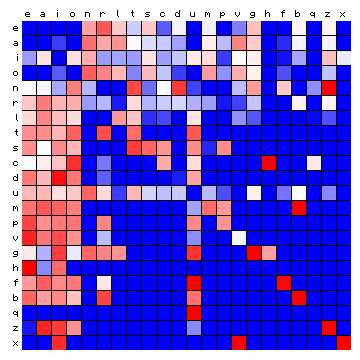 |
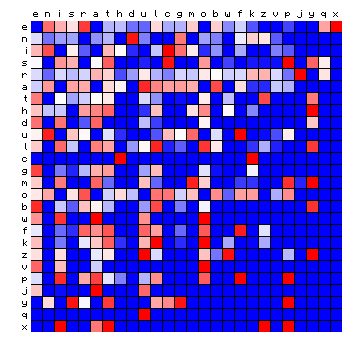 |
| C-D | FSG |
|---|---|
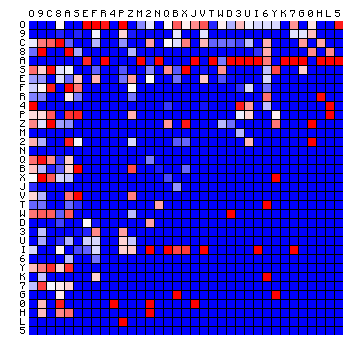 |
 |
| ZL (Eva) | ZL (Cuva) |
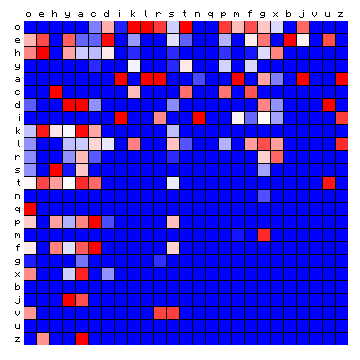 |
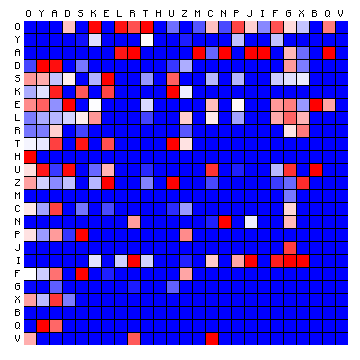 |
Figure 11: relative character pair distributions for all 8 sample texts
A few observations from these plots may be highlighted:
It was stated before that, in case the characters in a text are independent from the preceding character, the character pair entropy has a value which is twice the single character entropy. In reality they are of course dependent, as all the plots have clearly shown, so the character pair entropy is less than twice the single character entropy. We may call 'conditional character entropy' the difference between character pair entropy and single character entropy. It follows that the conditional character entropy is less than the single character entropy. The following table gives the values for the 8 cases.
| Text | Language | Character entropy |
Conditional entropy |
|---|---|---|---|
| Voynich MS (part) | C-D transcr | 3.857 | 2.085 |
| Voynich MS | FSG transcr | 3.829 | 2.052 |
| Voynich MS | ZL transcr (Eva) | 3.862 | 1.836 |
| Voynich MS | ZL transcr (Cuva) | 3.872 | 2.124 |
| Mattioli | Latin (16th cent) | 4.036 | 3.234 |
| Pliny | Latin (classical) | 3.998 | 3.266 |
| Dante | Italian (14th cent) | 4.014 | 3.126 |
| Tristan | German (modern) | 4.022 | 3.039 |
Table 2: conditional character entropy of some plain text in three languages,
and of various translitterations of the Voynich MS text.
In this case, the differences between Voynich text and plain texts in Latin, Italian and German are quite spectacular, and reflect the significant differences seen in the plots. Also these tabular values may be plotted against each other, with the single character entropy on the horizontal scale and the conditional character entropy on the vertical scale (see Figure 12 below). It is immediately obvious that the difference between the various known languages is much smaller than the difference between Voynich text and any of these languages. The single point among those for the Voynich MS text files that is somewhat separated from the other three is for the ZL translitteration that uses the Eva translitteration alphabet, which tends to represent some of the script characters by pairs of translitteration characters, and this result was to be expected. It also shows that the use of the Cuva alphabet effectively resolves this issue.
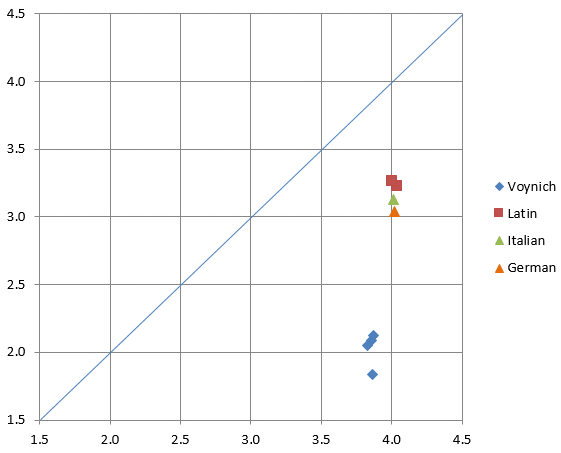
Figure 12: conditional character entropy (vertical) vs. single character entropy (horizontal)
A very important conclusion from this Figure is, that the different translitteration alphabets show a similar result, and this result is therefore representative for the writing in the Voynich MS. Even though the Currier alphabet and the Eva alphabet have completely different definitions of what is 'one single symbol', (and FSG and Cuva are probably closest to the truth), the statistics are similar, and quite far away from those of 'normal languages'.
The plots for the plain languages are dominated by the alternation of vowels and consonants, and the fact that such combinations are the ones that tend to have the highest frequencies. The plot for the German text "Tristan" looks somewhat different from the other three, because there are more consonants among the highest-frequency characters. It is of interest to redo the plots by separating the vowels from the consonants. For the known languages this can be done easily, but for the text of the Voynich MS we do not know which characters are vowels and which are consonants, or in fact if the characters in the Voynich MS alphabet can really be separated in this way.
This problem can be approached by applying a two-state Hidden Markov Model (HMM) to all texts. This technique has been introduced briefly with a brief introductory description. The experimentation with this topic is discussed in a dedicated page, which is still under work.
It was already mentioned in the course of this page, that the Voynich MS text is definitely not a Latin text that has been transcribed using an invented alphabet (simple substitution). However, we should also keep in mind what has been discussed on the previous page, namely that there is a whole tree structure of possible ways in which the Voynich MS text may have been composed. An encoding of a Latin text by simple substitution is just one very specific example that is based on several different assumptions. For the present purpose we may separate all cases into the following two larger classes:
A small digression follows, just to give an example of a 'process without a plain text'.
An interesting set of experiments in Bennett (see note 1), is what he refers to as "Monkeys" (7). These are Markov processes that generate random texts (as if a monkey was arbitrarily punching on a typewriter), though with pre-defined statistical properties. A "first-order monkey" would generate texts with a predefined character distribution. A "second-order monkey" would generate texts with a pre-defined character pair distribution. Examples of this are provided on this page.
The interesting part of this is that such an automatically generated text would be meaningless, but have exactly the same character distributions as shown in all the above plots. The first-order monkey would generate the plots that appear on the right-hand side of Figures 7 and 9. The second-order monkey would generate the left-hand side of these. As Bennett further illustrates, higher-order monkeys would generate texts that start showing some words in the language that was used to define the statistical properties of the monkey.
It is not realistic to assume that a medieval jokester would have done this. However, it just shows that there is a way to randomly generate text through some 'process', rather than converting a real plain text. If this was done, then the entropies and character distributions we are observing are those of the process, so we would need to look for a process that has these properties. In other words, when experimenting with processes, we can check how close they are to generating these properties.
Let us now look at the more interesting case that the Voynich MS text was generated by taking some plain text in some language, and applying a process to it resulting in the text we have. We don't yet know the language, and the process may have been a cipher or something else. The original text had its entropy and its character pair distribution, but the process could have modified it. This basically leaves two options:
To make matters more complicated, intermediate possibilities also exist, whereby the original entropy was already smaller (i.e. the character combinations already much reduced), and the process did not (need to) reduce it by too much. Furthermore, the 'process' may have consisted of several steps, each with its own impact on the entropy. We already know that one of these steps involved rendering the text in an invented alphabet, but if that was a simple substitution step 'at the end', this had no impact on the statistics shown on this page, so these have to be explained by any or all previous steps.
Only three languages have been analysed here, one of which (German) was a modern text, but it should be clear that any similar language, i.e. one with a similar alternation of vowels and consonants, will not make any significant difference. Looking again at Figure 12, we see that such a language will not bring us anywhere nearer to the Voynich MS text properties. We either need a drastically different language, or a 'conversion method' that makes drastic changes to the character distribution.
Time for another short intermezzo or two.
Numerous 'solutions' to the Voynich MS text have been proposed that involve expansion of abbreviations as are frequently found in medieval MS texts. This means that the text is proposed to be similar to a simple substitution of a Latin text (which we already know cannot work), but with the additional feature that certain characters of the Voynich MS text should be expanded to combinations of plain text characters. Typically, it is proposed that the Voynich MS symbol should be translated as "us". This is consistent with actual historical usage.
Would this expansion of characters be able to explain the difference we have seen in the plots above? The answer is a very firm: no! There are several reasons for this.
The main point is a general statistical one, from information theory. Compression of a string of characters means an increase in entropy, while the inverted process (de-compression of the compressed file) a decrease in entropy. Thus, a process converting a plain text with higher entropy to the Voynich MS text is equivalent with some kind of expansion. Now, replacing Voynich MS characters with further expansion will not increase the entropy, but rather reduce it (8). Because of what has just been described here, the Voynich MS text has occasionally been called (or compared with) a verbose cipher (9).
The above explanation may be illustrated by looking more closely at the results for the ZL translitteration in the Eva and Cuva alphabets. Starting from the Cuva translitteration, the Eva translitteration is exactly like a verbose cipher:
The Eva plots in Figures 11 and 15 tend to be more sporadically filled than the Cuva plots, even though the difference is not very great. Likewise, expansion of the Voynich MS text by assuming that there are abbreviations will have a small, similar, effect. It will not be capable of 'filling up all the gaps', in order to arrive at something similar to the plots for plain Latin.
All entropy calculations that have been presented are based on a written text. There have long been suggestions that the Voynich MS could be a (first) rendition in writing of a language that was never written before. In this case, the writing in the Voynich MS should more closely follow a spoken text. For many languages, the written text may differ considerably from the spoken text. Consider the phoneme which is written in Czech as š, in English as sh and in German as sch. This is 1, 2 or 3 characters for the same phoneme.
This means that not all conclusions drawn from comparisons with written texts may be valid for a close approximation of a spoken text. However, the issue already identified: the very restricted combinations of vowels and consonants, remains. Until someone finds a good way of experimenting with this, we need to keep in mind this caveat.
Based on what has been written above, the task of explaining the Voynich MS text and its properties may be one of the following:
In this section we will look at option 2. While this is only one of three options, for many people this is considered the fundamental question about the Voynich MS: to find the language. Looking back at Figure 12, we see that the Voynich MS text is completely different from Latin, Italian or German. Other closely related languages and dialects will not make any significant difference, so we need to look for a very different language.
Bennett (see note 1) included a number of other languages is his analysis, but found no good match, with the exception of Hawaiian. This language is not a very likely candidate for the source language of the Voynich MS text. Reddy and Knight (10) find that the predictability of characters, derived from entropy, is similar to Chinese transliterated in Pinyin. Both points indicate that there are languages that are very significantly different from Latin/English/German in terms of entropy.
A priori, some languages are more likely than others as a potential source for the Voynich MS text. Greek, Hebrew, several languages using the Arabic script, Coptic or Armenian are all reasonable candidates, none of which have yet been subjected to dedicated entropy analyses, to the best of my knowledge (11). These tend to have in common that they do not use the Roman alphabet, and there could be various different ways that they could be converted to the set of 24-36 symbols that we see in the MS.
This means that for some languages to be tested, some 'process' is automatically implied from the start. This is the process to convert the symbols of its writing system into the alphabetical sequence used in the Voynich MS. This quickly gives rise to a very large set of possibilities, and an enormous area for further research.
In a previous page I already computed the bigram entropy from sample texts in numerous languages. These texts are the 'Universal Declaration of Human Rights' that has been translated in to almost 400 different languages. The second Figure that is part of that description included a few points that were relatively near those for the Voynich MS. We may now look at some of these, namely:
| Code | Group | Language | Entropy | Comment |
|---|---|---|---|---|
| 016 | Asian | Minjiang | 2.390 | Alphabetic form of a Chinese dialect |
| GLA | Gaelic | Scottish | 2.642 | Uses non-standard Ascii characters |
| HAW | Asian | Hawaiian | 2.544 | Named by Bennett. Uses diacritics. |
| TGL | Asian | Tagalog | 2.372 | The closest statistics of all |
Table 3: some 'exotic' languages with known low entropy.
Below, I produce the standard 'relative frequency' plots for these cases. It should be noted that the font used for the legend cannot reproduce special characters, and for the time being these are all represented by a question mark (?).
| Minjiang (Chinese) | Scottish (Gaelic) |
|---|---|
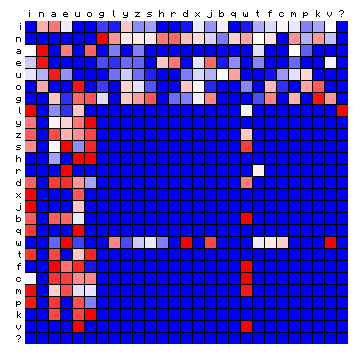 |
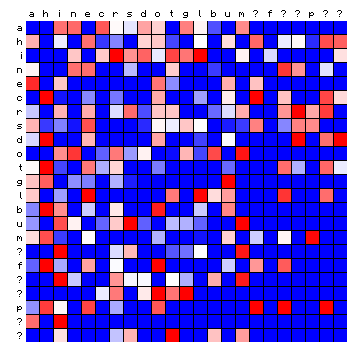 |
| Hawaiian | Tagalog (Philippines) |
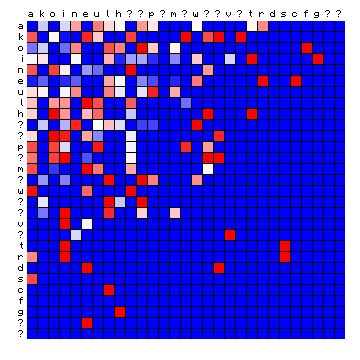 |
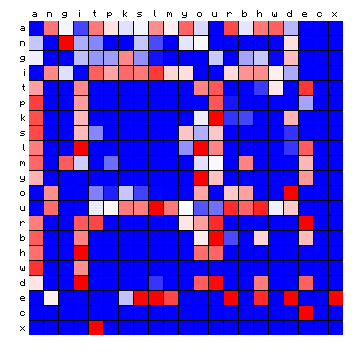 |
| Voynich (FSG) | Voynich (ZL - Cuva) |
 |
 |
Figure 13: relative character pair distributions for four 'exotic' languages.
Only a qualitative impression can be provided at this point. The cases of Minjiang and Tagalog show large blocks that are completely 'empty'. The Scottish and Hawaiian examples appear qualitatively more similar to the Voynich MS text. It should be possible to say more about these cases after a tentative vowel/consonant separation.
We have seen in the above discussion, and in particular in the various Figures, that the way in which character pairs are formed in the Voynich MS is completely different from that in known plain texts in Latin, Italian and German. This difference is reflected in a single number which is the conditional character entropy. While it has long been known that the conditional character entropy of the Voynich MS text is anomalously low, the importance of this is not realised properly by most would-be deciphers of the Voynich MS text.
Character entropy values have been computed for many texts in other languages, and they are found to be mostly similar to those presented in the present page. So even if we do not have the detailed character pair distribution graphs for all of them, we can safely conclude that the problem is the same. On a later page related to Hidden Markov Modelling, we will see that this conclusion is likely to be valid for all written languages that have a fairly normal alternation of vowels and consonants.
This only means that it is not useful to search for a solution that is exclusively (or largely) based on simple character substitution. More generally, the solution could be contained in any of the three following areas:
 |
 |
 |
 |