Special Topics: Analysis of the text

The main page related to statistical text analysis is here. The present page has the following topics:

How many characters, how many words?
Strings of i's
Definition of the "Cuva" analysis alphabet

How many characters, how many words?

Introduction

The most elementary statistics of the Voynich MS text are the number of characters and the number of words in the MS. No authoritative figures for this have been published, but based on the available transliterations, they will be derived here. Both numbers are uncertain, because of the uncertainty in the definition of the character set in the MS, and the uncertainty about word spaces. Both statistics can be derived from transliteration files, the completeness of which has been reported here. The GC and ZL files are the most suitable for this purpose (1).

How many characters?

The ZL transliteration is complete, but the Eva alphabet in which it has been expressed is not suitable for counting characters. We will come back to it below. The GC transliteration is 99.6% complete. It lacks only 22 loci, all of type "L" (label or single word). The v101 transliteration alphabet it uses has been designed to represent what its designer considered single characters by single transliteration characters. Counting the symbol for unknown characters: "?" as a single character, and not counting certain or uncertain spaces, this transliteration includes 158,959 characters. For the 22 missing labels we may add an estimated 130 characters, bringing the estimated total to 159,089 which we may round to 159,100.

To count characters in the ZL transliteration file, all alternate readings are resolved to the first option, and ligature brackets { } are removed. The character count using Eva is 194,570 . In this count, all unreadable characters are counted as one, while unknown sequences of unreadable characters have been counted as three. In any case, this number is not particularly useful. To obtain a better count, the text may be converted to the Cuva alphabet as described further below, while deleting all 'quote' symbols. In this case, the count of characters becomes 166,232 .

The difference between the two numbers is rather large: about 7000, which is just over 4%. This is primarily due to the fact that all pedestalled gallows characters in the GC transliteration are counted as one character, while in the ZL transliteration they are counted as two or more. Since we don't know what is the truth, the range of 160,000 to 165,000 may be considered our present best guess.

How many words?

This question concerns the number of word tokens. That is, if any word occurs 100 times in the MS, it is also counted as 100. The count is made difficult by the uncertainty of word spaces. Both the GC and ZL files indicate "certain" and "uncertain" spaces, so we can obtain two counts for each file. Since the results show a signficant difference, we will also use the IT transliteration file for this purpose. As shown elsewhere, this file includes 'only' 96.8% of all loci, but the missing loci tend to be short (mostly singles words), so the statistics will be only marginally affected by the roughly 200 words (which may be expected to be rare words). The IT file does not indicate "uncertain" spaces.

To count words, we should exclude loci of which we may argue that they do not represent words, but rather single characters, which typically appear in sequences. The exclusion criteria are listed here, for transparency, and so that others may repeat these counts. The following table lists the loci that have been excluded in the counts, and the reasons for this.

Fol.	Loci	Nr.	Reason	In GC / IT file?
f1r	all Lx	3	Individual characters in the margin, in a later hand.	No / 0
f11v	5,*L0	1	Two characters in the left margin	No / 0
f17r	@Lx	1	Marginal writing not counted	No / 0
f49v	All L0	26	Individual characters	Yes / 26
f57v	3,@Cc	1	Individual characters	Yes / 1
f57v	5,@Cc	(1)	Only the part that consists of single characters	Yes / (1)
f66r	16-49	34	Single characters	Yes / 34
f75v	All L0	6	Single characters	Yes / 6
f76r	All L0	9	Single characters	Yes / 9

Table 1: Loci that have been excluded when counting words

The following table gives the different counts:

Transliteration	Counting uncertain spaces	Skipping uncertain spaces
GC	40,530	38,071
ZL	38,805	36,072
TT	-	36,940

Table 2: word counts in the Voynich MS

The differences are rather large. This difference is not explained by the different transliteration alphabets used, but by the different interpretation of what are word spaces. GC "sees" more spaces than ZL and TT, and the complete set of "certain" spaces in the GC transliteration is roughly the same as the combination of "certain" and "uncertain" spaces in ZL. Overall, GC has about 5% more words in both cases. Just to present an indicative number, one may say that the Voynich MS includes roughly 37,000 - 39,000 word tokens (words).

How many different words?

This question concerns the number of word types. That is, if any word occurs 100 times in the MS, it counts as 1. The number is again computed for the above four cases.

Transliteration	Counting uncertain spaces	Skipping uncertain spaces
GC	9,814	10,553
ZL	8,412	9,467
TT	-	8,545

Table 3: word type counts in the Voynich MS

If one considers the uncertain spaces as word spaces, then, of course, there are more word tokens in the transliteration than if one counts only the certain ones, as already observed above. Interestingly, however, in that case there are at the same time fewer word types (different words). This rather surprising result is found both for the GC transliteration and the ZL transliteration. Effectively, it means that the indicated "uncertain" spaces in both files tend to split longer words into shorter words that appear with some frequency.

Again, the numbers are quite different. In this case, the ratio between GC and ZL is well over 10%. This increase in the difference is caused by the transliteration alphabet. As a typical example, GC considers several different forms of the Sh character, giving rise to a larger number of different words. A representative number of word types may be 9,000 - 10,000.

Strings of i's

Introduction

While the writing of the Voynich MS is generally unusual, there are probably two features that really stand out. One is the use of so-called gallows characters, which can be combined with so-called benches or pedestals. This has been described here. The other is the fact that characters are rarely duplicated except for e and i, which can even occur in sequences up to four instances. It is the latter that we will look into here. These sequences are a real challenge for those who are interested in transliterating the text. The statistics presented below may support decisions on a suitable way to transliterate and/or interpret these strings. In the following, I will refer to the i's and c's as "symbols", leaving open the question whether these are intended as characters, or whether they are just parts of characters (minims).

General appearance and transliteration

The strings of "i" tend to occur near the ends of words. When they are at the end of a word, they are essentially always (2) followed by the symbol n, which may very well be nothing else than the word-final version of i, but of course we can't be certain. In numerous cases, the last symbol is not n but r, and also l and m, occur in that position, but much more rarely. It should be noted that all this is true for strings of "i" of all lengths, though the long strings are rare and for the case of 3 or more "i" not all combinations exist.

For this reason, in historical transliterations of the Voynich MS different approaches were taken when representing these strings. Referring to Tables 1, 3, 6 and 7 on the transliteration page, following is a summary comparison of the Currier, Eva and v101 methods.

Cur.	Eva	v101	Cur.	Eva	v101	Cur.	Eva	v101	Cur.	Eva	v101
D	n	N	2	r	y	E	l	e	J	m	p
N	in	n	T	ir	z	G	il	(ie)	K	im	P
M	iin	m	U	iir	Z	H	iil	(Ie)	L	iim	q
3	iiin	M	0	iiir	(Iz)	1	iiil	(3)	5	iiim	-

Table 4: Different transliterations of strings of "i"

For the cases where the v101 transliteration is between parentheses, these are codes that have not been specifically defined, but indicate how they are most commonly rendered in the GC transliteration file (4).

Note that for the strings of "c", combination codes have only been defined in v101, while both Currier and Eva transliterate then individually, e.g. "CCC" in Currier or FSG and "eee" in Eva.

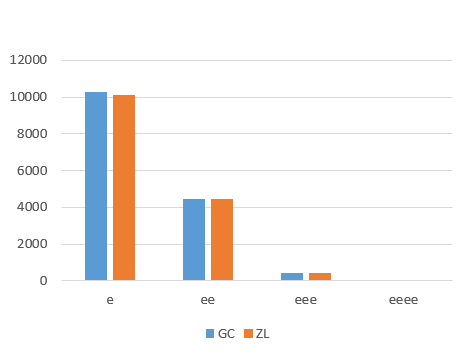
An important difference between strings of "i" versus strings of "c" may be illustrated first. This is related to the frequency distribution of the number of repeats. As indicated already above, for strings of "i" one may take two different approaches, namely counting the trailing "n" as an "i" or counting it as a different character. Following shows the distributions for the two main transliterations GC and ZL.

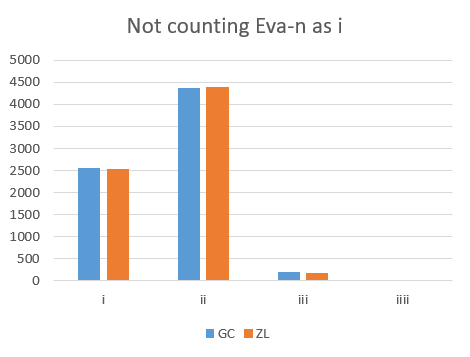
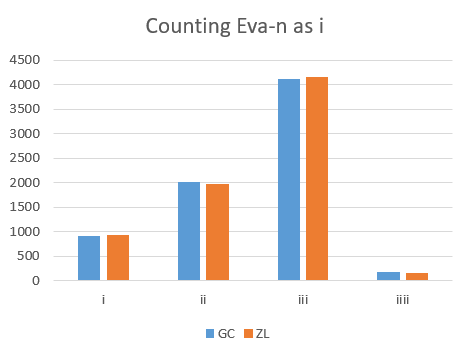
For the strings of "i", the highest frequency of occurrences is for length 2 or 3, depending whether the final "n" is included in the count. As we shall see below, this distribution is dominated by the frequent string "iin" or iin.

For the strings of "c", however, the frequency goes down monotonously as a function of the length. This clearly shows that strings of "i" and strings of "c" must have a different function, whatever this function is. With this we may leave the strings of "c" and concentrate on the strings of "i".

Counts

The following table shows the counts of the of strings of i in the ZL and GC transliterations (5). The counts for the individual symbols r, l and m are included for comparison, but these are strictly outside the scope of this analysis. Note that for the symbols/strings i, ii and iii the counts reflect the case where they are not followed by any of the characters listed in the top row. As a first observation, it is interesting to note the close correspondence between the numbers for these two independent, and completely different transliterations (6).

Symbol	ZL count					GC count
		140	6819	10607	1014		129	6602	10605	989
	110	1729	610	34	46	93	1759	610	37	52
	61	4148	162	14	11	88	4113	169	13	16
	8	166	2	4		10	180	2	1
		1					4

Table 5: Strings of "i" and their frequency in the Voynich MS

From these counts, we may make the following observations:

The symbol n differs from all the others in that it is predominantly preceded by strings of "i" of different length. It can stand alone but this is relatively rare (ca. 2%). For the other symbols it is exactly the opposite. This strongly supports the notion that this symbol is indeed a word-final version of i (7).
The most frequent combination is "iin" and the second most frequent is "in". Using the ZL transliteration, "iin" accounts for 58.3% of all cases, "in" for 24.3% and all others combined for 17.4%.
The strings ending in "r" are still relatively frequent. Especially "ir" and "iir" clearly outnumber the cases where "i" and "ii" are followed by any other character. The strings ending in "r" also visually resemble the strings ending in "n" and there are numerous places in the MS where some intermediate form exists and the reading is very difficult. We must remain in doubt whether "iir" is more like "ii" + "r" or like "iin" + "r".
The strings ending in "l" or "m" are quite rare, compared both to the individual characters and to strings of "i" ending with other symbols. As an example, iid is as frequent as iil or iim.

Definition of the "Cuva" analysis alphabet

Introduction

In general, text analyses are made difficult by our uncertainty what is a single character in the Voynich script, and in fact such analyses may help in answering that question. The Eva transliteration alphabet, which has been defined here, was specifically targeted to allow a transliteration of the text of the Voynich MS in a simple but consistent form. Its design does not make it suitable for text analyses. It represents some Voynich character shapes that are most probably meant to be single characters by two or even more transliteration characters (for example 'ch' for ch and 'iin' for iin ). Note that the Currier alphabet quite probably has the opposite problem.

In order to do some types of text analyses (in particular those where it is important to identify single characters), an alphabet derived from Eva will be used, for transliterations based on Eva. While there are many possible choices, and it is worth experimenting with different options, for consistency I will show here a single example, which is in a way a mixture of Eva and Currier, which I will therefore refer to as 'Cuva'.

Note that this is not intended to represent a good transliteration of the Voynich MS text. It is made purely for reasons of text analysis.

Cuva alphabet table

	Currier	Eva	Cuva		Currier	Eva	Cuva		Currier	Eva	Cuva
q	4	q	H	cFh	Y	cfh	FS	im	K	im	IJ
o	O	o	O	a	A	a	A	iim	L	iim	NJ
d	8	d	D	e	C	e	E	iiim	5	iiim	MJ
y	9	y	Y	i	I	i	I	g	6	g	G
s	2	s	C	il	G	il	IL	j	7	j	Q
l	E	l	L	iil	H	iil	NL	x		x	X
ch	S	ch	S	iiil	1	iiil	ML	v		v	V
Sh	Z	sh	Z	ir	T	ir	IR	r	R	r	R
t	P	t	T	iir	U	iir	NR	b		b	B
p	B	p	P	iiir	0	iiir	MR	u		u	A
k	F	k	K	n	D	n	I	z		z	J
f	V	f	F	in	N	in	N	ee	CC	ee	U
cTh	Q	cth	TS	iin	M	iin	M	eee	CCC	eee	UE
cPh	W	cph	PS	iiin	3	iiin	NN	eeee	CCCC	eeee	UU
cKh	X	ckh	KS	m	J	m	J

Table 6: Definition of the Cuva analysis alphabet

To convert files in (Basic) Eva into Cuva, the most convenient way is using a general tool ('bitrans') that is presented here. The corresponding 'rules file' for this conversion is provided here.

With the recent availability of transliterations in the STA alphabet, and the bitrans tool, it is now straightforward to build much more advanced and complete analysis alphabets.

Notes

1: For the meaning of the codes ZL, GC and later also IT, see the page about transliteration of the MS.
2: Terms like 'usually', 'almost always' and 'essentially always' always tend to be accompanied by exceptions, i.e. there does not seem to be any rule related to the text of the Voynich MS that is truly valid without exception.
3: This combination appears only once in the GC file and is transliterated as the high-ascii code 181 followed by e. In IVTFF notation: @181;e .
4: Note that the GC transliteration also uses: "iN" to transliterata Eva-"in"; "in" for Eva-"iin"; "iy" for Eva-"ir"; "Iy" or "iz" for Eva-"iir" and several more.
5: The counts for ZL are based on file version 1q of 02/04/2020.
6: The relatively large difference in the counts for Eva-r (3.2%) is caused by the fact that the v101 alphabet recognises a number of slightly different versions of this letter, which are not included in this count.
7: It is tempting, and even necessary, to take into account the word boundaries in this analysis, but due to the reltively low reliability of existing transliterations with respect to word boudnaries, this is not yet attempted here.