From bigram entropy to word entropy in the Voynich MS

Introduction

Both first and second order entropies of the text of the Voynich MS are lower than that of Latin or English, as has been shown here. In addition to that, the words in the Voynich MS tend to be relatively short (1). Thus, one would expect Voynichese words to be more restricted or less diverse than words in Latin. This word diversity can be measured either by counting the number of different word types for texts of various lengths, or by computing the single word entropy from the word frequency distribution. Both statistics have some shortcomings: the number of word types is affected by spelling or transliteration errors and the single word entropy can only be estimated from long texts. In the following, both statistics will be computed for texts in Voynichese and in other languages, using samples of the same length (counted in number of words) to minimise these problems.

A long section of Voynich MS text has a single word entropy of roughly 10 bits, just like normal language (2). Thus, an apparent contradiction appears. How can it be that the text of the Voynich MS uses shorter words, with less variability in the character combinations, yet still produces a normal variety of words? Investigating this question is the purpose of the present page.

This was first written in 1998, and the graphics were rather difficult to understand. The present version is a complete remake from 2019. It does not yet include all the material that was in the original version. Analysis of texts in some 'exotic' languages (Dalgarno's, Pinyin) is still missing for the time being.

Description of the numerical analysis

We will look at the characters that compose a text, as they appear from the start of a word token, and also at entire word tokens. The appearance of each of these items is an event with a probability p(i), which has a value between 0 and 1. This probability can be estimated by computing the ratio of the number of times n(i) that this item occurs, and the total number of items Ntot:

p(i) = n(i) / Ntot

The amount of information that is obtained if this item occurs, expressed in bits, equals:

b(i) = - log₂ (p(i))

using the logarithm of base 2 (3). What does this mean? Let's assume that a certain word has a frequency of appearance in a piece of text of 1/512. This is the same as saying that the probability of this word appearing in any position of the text is 1/512. Consequently, and knowing that 512 is 2⁹, the appearance of this word provides us with 9 bits of information.

We may also take the average number of bits of information over all word tokens in the text:

H_W = { SUM n(i) * b(i) }/Ntot  = SUM p(i) * b(i) 


H_W = - SUM p(i) log₂ (p(i))

This is the standard formula for entropy, and H_W is the symbol we use for the single word entropy.

The bits of information can be considered to be distributed over all characters of the word. Let us look at the appearance of the English word 'the' at some position in a text. In the following I will use a colon (:) to mark the start of a word, and a period (.) to mark the space character after the end of the word. The probability p(':the.') of this appearance can be calculated (trivially) as:

p(:the.) = p(:t) * p(:th)/p(:t) * p(:the)/p(:th) * p(:the.)/p(:the)

Each of the ratios in this product represents a conditional probability p(A|B), namely the probability of 'A', given condition 'B', counting from the start of the word.

p(:the.) = p(:t) * p(:th|:t) * p(:the|:th) * p(:the.|:the)

Taking the base-2 logarithm of the earlier expression leads to the following (again trivial) equation for the number of bits:

b(:the.) = b(:t) + b(:th)-b(:t) + b(:the)-b(:th) + b(:the.)-b(:the)

It is more interesting to take the average of all words, and this is achieved by replacing the number of bits for one token by the corresponding entropy values.

In the present study, the text of the Voynich MS will be compared with some plain texts in known languages, for the first characters (1 to 4) and for words.

One practical consideration is how to combine the statistics of words of different lengths. To solve this, all words are considered to end with an infinite number of trailing spaces. The first space at the end of a word (the period used above, in ':the.') is a significant character. It tells the reader that the word ends here, and it is not part of a longer word like 'them' or 'these'. All remaining spaces contain no further information, as the probability of a space following a space equals one, and its contribution to the entropy is zero.

First results (short texts)

Let us first analyse the text in the Voynich MS for each apparent section separately, as we already know that the text properties are not uniform throughout the MS. Clearly, the most reliable results will be obtained from analysing long texts, but the various sections of the Voynich MS are relatively short. We will look at both the number of item types, and the entropy values, as a function of the text length (number of word tokens). The item types are word-initial n-grams and complete words. For the Voynich MS text these calculations have been made based on the ZL transliteration, using the Eva transliteration alphabet (4). The graphics use the following colour scheme.

red	Voynich MS Herbal text in Currier A language
cyan	Voynich MS Herbal text in Currier B language
blue	Voynich MS text in the stars section (quire 20)
magenta	Voynich MS text in the biological section (quire 13)
green	Dante (Italian)
grey	Pliny (Latin)

Table 1: Colour definitions for the Figures in this page.

The following graphic shows how the set of different word-initial N-grams and the word types increase as a function of text length. This shows 'counts'.

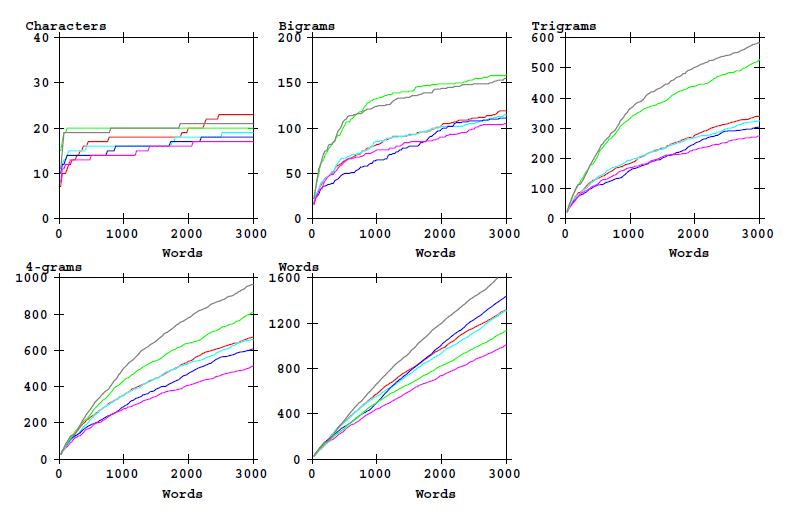
Figure 1: Counts of word-initial characters bigrams, etc, and of word types as a function of text length. Eva transciption alphabet.

The following graphic shows the evolving values of the entropy for the same quantities, as a function of text length.

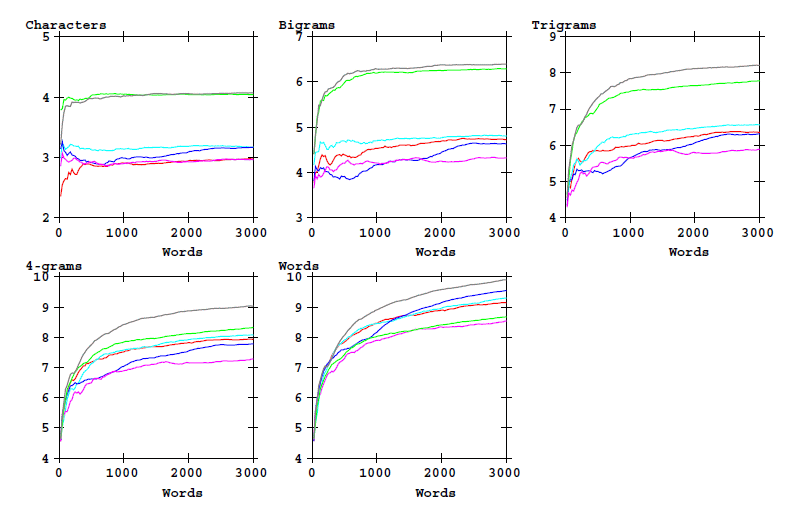
Figure 2: Entropy of word-initial characters bigrams, etc, and of word types as a function of text length. Eva transciption alphabet.

The Eva alphabet is not very well suited for statistical analyses, and the analysis has therefore been repeated for the same text sections converted to the Cuva alphabet.

Definition of the "Cuva" analysis alphabet

This is the corresponding graphic for the counts:

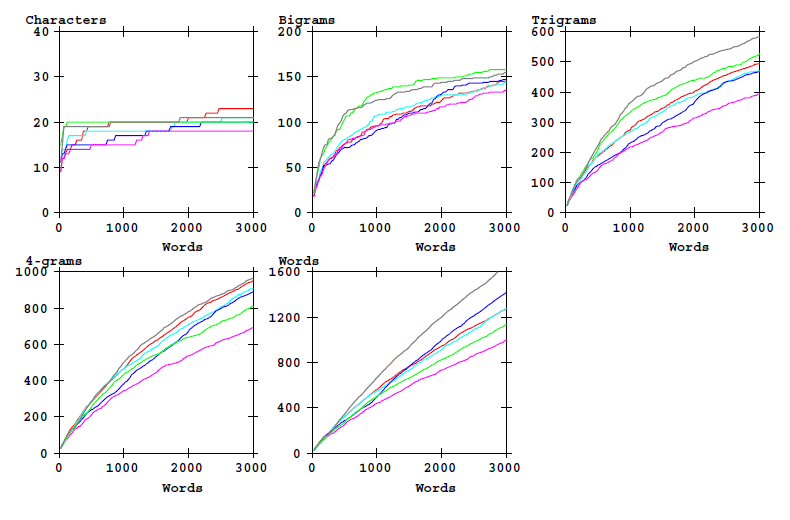
Figure 3: Counts of word-initial characters bigrams, etc, and of word types as a function of text length. Cuva transciption alphabet.

and for the entropy:

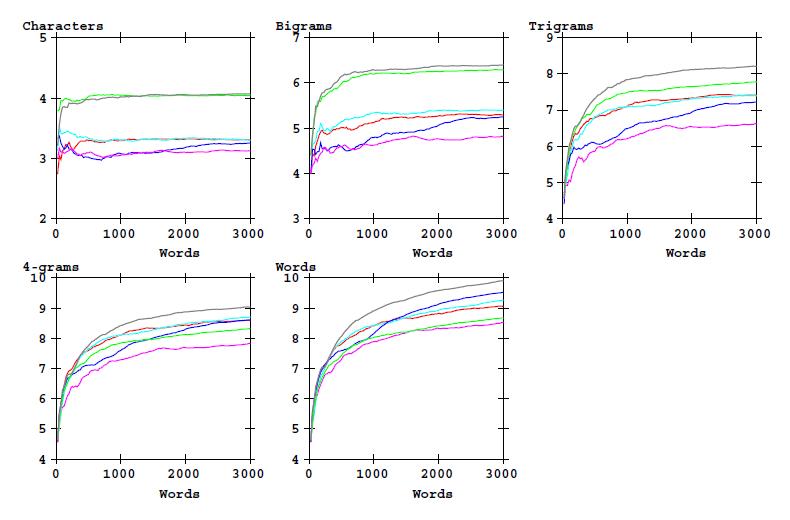
Figure 4: Entropy of word-initial characters bigrams, etc, and of word types as a function of text length. Cuva transciption alphabet.

Following are some initial observations. A more complete discussion is presented in the section 'Conclusions' further down.

The Voynich MS text (all sections) in the Cuva alphabet more closely resembles the two plain texts than the version in Eva. This suggests that Cuva better represents single characters in the Voynich MS.
Both the word type counts and the word entropies are essentially identical in Eva and Cuva, but the information per n-graph is lower in Eva than in Cuva, as expected.
Among the various sections in the Voynich Ms, the parts in 'herbal-A' and 'herbal-B' appear most similar to each other, in spite of the significant differences between the two Currier languages A and B.
The Voynich MS text is about as information-rich as Dante's Italian, but less so than Pliny the elder's Latin.
The Voynich MS text contains significantly less information in the first two characters of each word when compared with Italian or Latin, but compensates this by having greater variability in the trailer.

Results for longer texts

It is of interest to verify the above observations by using longer text samples. The longest consistent part in the Voynich MS is formed by the stars (recipes) section in Quire 20. The version in the Cuva alphabet is again compared with the plain texts of Dante and Pliny the elder.

The corresponding graphic for the counts:

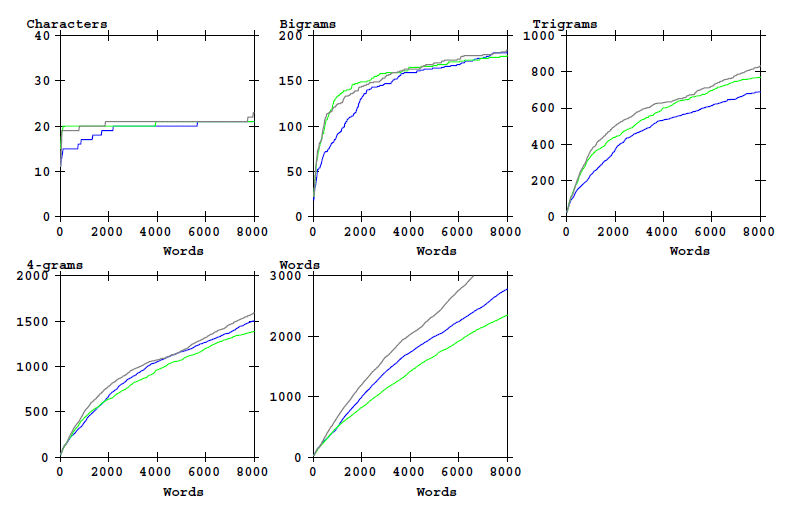
Figure 5: Counts of word-initial characters bigrams, etc, and of word types as a function of text length. Cuva transciption alphabet.

and for the entropy:

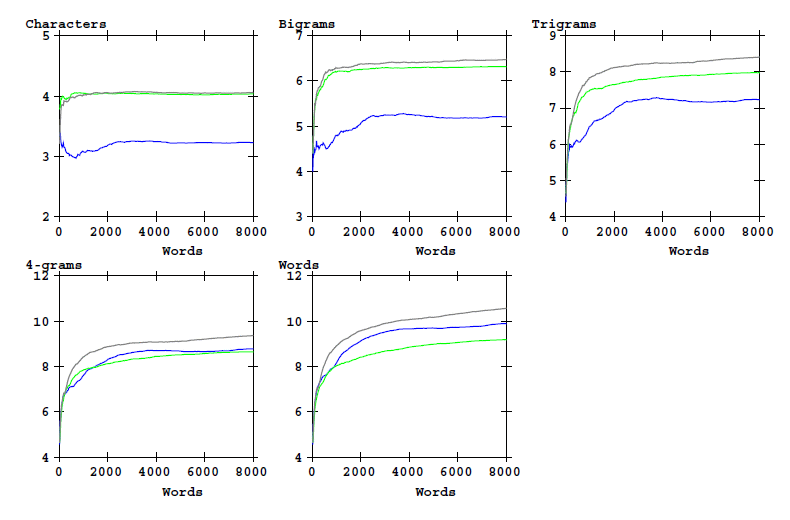
Figure 6: Entropy of word-initial characters bigrams, etc, and of word types as a function of text length. Cuva transciption alphabet.

Entropy per character

The following two tables provide the numerical values for the 'bits of information' as explained at the top of this page, for the first 8000 words of the three texts:

Characters. First:	1	2	3	4	All
Dante	4.0330	6.3181	7.9769	8.6565	9.1941
Pliny	4.0588	6.4742	8.4103	9.3736	10.5756
VMs stars	3.2298	5.2070	7.2367	8.7832	9.9019

Table 2: Cumulative bits of information.

Characters:	1st	2nd	3rd	4th	Rest
Dante	4.0330	2.2851	1.6588	0.6796	0.5376
Pliny	4.0588	2.4154	1.9361	0.9633	1.2020
VMs stars	3.2298	1.9772	2.0297	1.5465	1.1187

Table 3: Bits of information per character.

Interpretation

The above shows that:

The single word entropy of the Voynich MS is not anomalous. For the first 8000 words in Quire 20 we obtain a value of 9.9. It is in between the values for Dante and Pliny. This could be an argument in favour of the significance of word spaces.
First-character and second-character entropy of Voynich MS text are significantly low, and thus especially also the initial-bigram entropy. However, in Voynichese, the third character of each word is as unpredictable as the second, and the fourth contains much more information than is the case in Latin or Italian
Both the word counts and the variability (entropy) of the Voynich MS text in Quire 20 is in between Latin and Italian.
Overall, the information contained in Voynich MS words i similar to that in Latin or Italian words, but the information is more equally distributed over the characters while the words are shorter.

The last point above is rather remarkable. William Friedman thought that the Voynich MS could be in some early form of constructed language, and the above observations could be considered to point into this direction.

Conclusions

Following are the main tentative conclusions from the work that has been described above:

From a statistical point of view, the apparent words in the Voynich MS behave like 'real words'. They are as varied as the words in Latin/Italian texts of a similar length.
The first and second character of Voynich words (using the Cuva alphabet) have lower entropy than in Latin. The Voynich words contain more information from the third character onwards (in the conditional sense).
A word game-type algorothm to convert Latin to Voynichese must:
- Increase predictability of word starts
- Make words shorter
- Maintain the length of the vocabulary

Acknowledgments

To be redone.

Notes

1: As demonstrated e.g. by Gabriel Landini in a paper about Zipf's law. The reference is temporarily missing (see here).
2: No accurate value is know to me a priori, but the present page will produce one representative estimate. A summary of this statistic may be found here.
3: See the introduction to entropy.
4: For transliteration file formats and the definition of Eva in general see here. A link to the file used in the present page is included here.