



 |
 |
 |
 |
On the main page related to transliteration of the text a common format for storage of all known Voynich MS text transliterations was introduced. In addition, in the course of this discussion, I introduced the concept of a 'Super Transliteration Alphabet' that would capture many more details in the handwriting than included in the present alphabets (extended Eva and v101). Here, I will follow up on a related suggestion, made at the same page, of creating a superset of all existing alphabets, in order to be able to represent all existing transliterations using a single alphabet. In the following, this 'Super Transliteration Alphabet' will simply be referred to as 'STA'. The concept is illustrated in Figure 1.
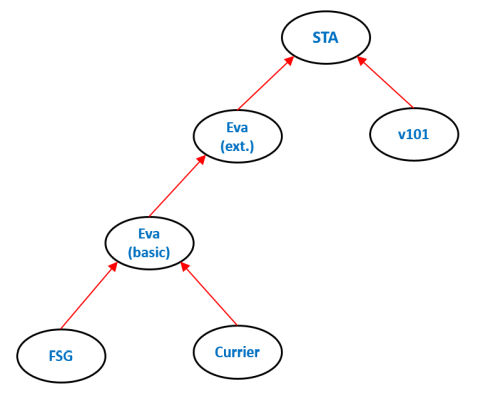
Figure 1: relationship between transliteration alphabets
It shows the dependencies of all main transliteration alphabets that are discussed at this site: Currier, FSG, Eva and v101. The arrows both mean: "is based on" and "fully includes", in the sense that the 'higher' alphabet can fully represent texts expressed in the 'lower' alphabet. In the opposite direction this is generally not the case. The figure shows that it is sufficient to make a superset of Extended Eva and v101, as this automatically captures all other alphabets. This means that the aim is not necessarily to create an alphabet with many hundreds or even thousands of slightly different symbols. Instead, we may choose to establish the smallest possible superset of extended Eva and v101.
This activity started in 2019, and after several iterations a reasonably stable version of this STA alphabet was established, which was also presented at the 2022 Voynich MS Conference, as part of the first keynote talk on 30 November: "Transliteration of the Voynich MS text" (1). A dedicated web page contains some additional material for that presentation and paper, also pertaining to the definition and use of the STA alphabet.
At the time of this presentation the definition of the STA alphabet was still a draft (numbered 16). Early 2023, this definition was modified and consolidated, and it is now identified as STA release 1, or "STA1".
There were two main questions and three minor questions that had to be resolved when setting up the STA alphabet. The two main questions were related to the overal representation of the characters:
Once these major points are resolved, there are three minor questions, or 'complications' in the Voynich writing system, for which each of the earlier alphabets has adopted different solutions:
Of the two inputs to STA, v101 is a synthetic alphabet (capturing all combined and/or ligatured characters as units), while Eva is analytical, defining the individual elements. In case the STA alphabet should be analytical as well, probably fewer different symbols would be needed, but all v101 characters would have to be broken up into their components resulting in something similar to extended Eva. In the other case, when STA is a synthetic alphabet, it will be necessary to find all possible combinations in extended Eva that exist in the ZL transliteration, such as, for example: {c@182;h}, which is a ligature of c, the rare character @182; and h. The second case would be a rather lengthy but straightforward process, while the first case would involve making numerous subjective decisions. It was therefore decided to make the STA alphabet synthetic. In the process of selecting all extended Eva composites, a total of 235 characters and combinations were found in the ZL transliteration file.
Note, that some time later also an analytical 'Super Alphabet' has been defined. This is at the other extreme: a highly analytical alphabet. Its definition relies entirely on the final definition of STA, and it is discussed on a separate page. Here, we will limit ourselves to the STA alphabet.
With v101 and extended Eva both having over 200 different characters, the combination will necessarily have even more, and it will no longer be possible to identify each character by a single byte. In addition, it has long been undesirable to use the high-Ascii area of the character set, something that was still prevalent in the 1990's despite its incompatibility with Unicode. The selected way forward has been to organise STA into 'character families'. Each family consists of a group of characters that are somehow similar in shape, and for which intermediate forms exist. Each character then consists of two identifiers: the family identifier and the 'family member' identifier.
Given that both the extended Eva alphabet and the v101 alphabet were defined in the course of a complete transliteration of the MS text, they exhibit a lot of similarity, and it has usually not been too difficult to match also the rare characters in both alphabets with each other.
One of the main mysteries of the Voynich MS script is the meaning of the pedestalled gallows. Since it was decided above to make the STA alphabet synthetic, this means that all possible ligatures involving gallows will become individual characters, so this decision has essentially been made already at that point. This again implies that we cannot conclude that individual STA characters represent single characters in the Voynich MS. STA characters can represent long ligatures (or rather: ligature-like strings) and are therefore rather likely to represent more than one single character in the writing of the MS.
The shapes, characters or minims and are the only ones in the Voynich MS writing that can frequently be found doubled, tripled or even more. Especially the strings of "i" look very much like minims and all alphabets prior to Eva would transliterate as "N" and as "M". At the same time, by itself also exists, but is much less frequent. The other thing all alphabets (up to and including Eva) agreed on is to treat all sequences of as sequences, not as composites.
It becomes more complicated when we consider that also characters like , , , etc. exist. Currier decided to provide a single character representation for each of them, whereas Eva writes them all out as minims. On the other hand FSG and v101 provided intermediate solutions where some cases are single composites and others are strings. In both latter cases, it is generally possible to represent these strings of "i" in different ways. While at first sight the Currier representation appears to be fully consistent, this is not really true, because strings of "i" can also be followed by other characters than the above-mentioned four, for example as: . In this case, Currier transliterates as "II8".
This means that only the fully analytical approach can be fully consistent, but we have just decided to create a synthetic alphabet. How to 'break up' the strings of "i" into meaningful components? To answer this question, I decided to look more closely into the statistics of these characters. This is described here in considerable detail. The short summary is, that it is reasonable to consider , , , etc. as composite characters, but not , (etc.), as these are even less frequent than other cases that Currier did not consider single characters, for example or .
Based on all of the above, a set of character families has been identified, where each family consists of characters that may also have intermediate forms. Thus, three of the most frequent characters: , and end up in the same family. Each family is identified by a single capital character, while family members are identified by:
This means that a transliteration in STA consists of only plain Ascii characters, and that, in principle, 26 x 36 = 936 different shapes can be represented.
The definition of STA families including the most important family members is provided in this PDF document. Inevitably, there could be many other equivalent results, but this design stems mostly from the Voynich MS text complications that have been described above. For the intruding gallows there are so many different versions that they have been split into three families each. This way it could be avoided that we need more than two bytes for each Voynich character.
The STA versions of the main characters in the Voynich alphabet, as identified in Currier, FSG and basic Eva, are listed in this PDF document.
Both the identification of the different families, and the list of members in each family, has been achieved through an iterative process. This would have been an impossible task without a software tool to convert transliterations between different alphabets. This tool will receive some attention further below. The first stable STA definition (STA-1) corresponds with the 17th iteration of this process, and is included in this PDF document.
An example of Voynich MS text expressed in STA is included in the follwoing figure. The top row includes a short line of writing that was taken from the fifth line of f36v.

Figure 2: from different native alphabets to a common alphabet (STA)
The second row shows the representation of this line in five different original transliterations, but represented in the IVTFF file format, while in the bottom row all text has been converted to the STA alphabet. Here, grey boxes indicate the remaining differences between the various transliterations.
This demonstrates several aspects. The first is, that this transliteration is not suitable for human reading, but only for computer processing. The second is, that transliterations will tend to be consistent in the choice of character family, but mostly differ in the choice of family member for each character.
Furthermore, to process STA files directly (e.g. to do statistics on the text) dedicated tools will be needed, because undoubtedly the majority of existing user tools expect to process transliterations with one character per Voynich MS symbol. However, in most cases users or analysts are less interested in very large character sets anyway, so for processing STA transliteration files a different approach is recommended, for which also see below.
It is important to stress here, that the STA alphabet is not meant to be the 'new transliteration alphabet that shall replace all previous alphabets'. Also, the alphabet shown and used here is not meant in any way as a definitive result. The unknown aspects of the Voynich MS writing system still remain. We cannot yet predict what is the 'correct' alphabet, and we cannot yet identify which are the individual characters. STA is primarily a new tool that will facilitate comparison of existing files and give more easy access to the full flexibility of the ZL and GC transliterations. Furthermore, we already saw that this alphabet is not suitable for human interpretation, and undoubtedly Eva will keep its role as an easy means of communication between users.
Having the transliteration files expressed in STA, combined with some useful software tools, allows users to easily define and create their own transliteration alphabets. Just like the files in STA were created from the original transliterations using a piece of software, the same software can be used to convert all transliterations to a user-defined alphabet. The tool that I have used for this purpose is called bitrans. It is freely available via this web page, which provides the source code in C and the user guide. The guide includes easy examples. The tool uses bi-directinal conversion tables called "rules files", and a great collection of existing rules files is already available. Examples are given in my 2022 Voynich conference paper (see note 1).
The fundamental requirement that all existing transliterations must be convertible to STA implies that this must not lead to loss of information. This can be verified by making the back conversion, which should result in an exact copy of the original file. When doing this test, issues appear with both the CD and the GC transliterations, which need to be dealt with. The case of the CD transliteration can be used to demonstrate this.
The following table shows a few Voynich character sequences, their Currier representation and their STA representation based on the decisions described above.
| Character | Currier | STA |
|---|---|---|
| | G | E1 B2 |
| | H | F2 B2 |
| | 1 | G2 B2 |
Now the CD file includes, in the transliteration of locus f23v.1, the word: O8AIIIE9 (Eva: odaiiily). Strictly speaking, this should have been transliterated by Currier as O8A19, if we follow his own rules. And indeed, converting the actual representation (8AIIIE9) to STA (B1 A3 G2 B2 A2), and then back to Currier, results in a change into this 'correct' code (O8A19). It is likely that this was a mistake by Currier, and it is also the only case that appears in the CD file. It would in principle be possible to record this as a mistake and modify the original file, but similar issues related to strings of "i" ending with or appear several times in the GC file, namely as follows:
In the case of this transliteration, it is not possible to assume that these are mistakes, but these were certainly intentional choices. Both issues can be resolved by identifying separate STA codes for the characters that are included in the strings of "i" ending with and . We may call these the 'bound' versions of these characters. Specifically:
| Character | Normal STA | 'Bound' STA |
|---|---|---|
| | B2 | B7 |
| | B3 | B8 |
| | E1 | E3 |
| | F2 | F5 |
| | G2 | G4 |
We now have the problem that these characters will appear in STA-encoded files as different characters, which was almost certainly not intended by the transcriber. This can be resolved by implementing a 'regularisation' step. If we consider the use of the codes B7, B8, etc. for these cases as 'level 0' STA (= most complete), it can be regularised to 'level 1' STA by substituting B7 by B2, B7 by B3, etc. The level-0 STA file can be reverted back to the original file, but the level-1 STA file cannot, because the distinction between bound and unbound characters is lost.
Use of level-0 STA in the Currier file results in translation of Currier: 8AIIIE9 to STA: B1 A3 G4 B7 A2, which then converts back to Currier 8AIIIE9.
In the STA definition tables, those codes that exist only in level-0 STA are highlighted in light purple. Users may decide which STA level they wish to use for their analyses. For most normal uses, level-1 STA will be most appropriate. For the FG, IT and ZL files there is no difference between level-0 and level-1.
Further regularisation
With the above-mentioned definition of level-0 and level-1 STA and the corresponding regularisation procedure, all issues with the CD file are resolved. There remain, however, further similar 'issues' with the GC file, in that there are several different representations of other strings of "i". These were intended by the transcriber, because he was particularly interesting in identifing in the MS which characters were intended by the original author(s)/scribe(s) as single characters. It is of course doubtful that this aim could be achieved, as the identification depends on minute differences in the spacing between characters and the presence of tiny 'hooks' on the characters. Unlike the issue described above, this is not causing any problems with conversion between STA and the original v101 alphabet. However, many users are likely to prefer to treat similar strings of "i" with similar representations. Following is a complete list of cases that may be found in the GC file:
| Character | Standard v101 |
Alt. v101 | STA | Alt. STA |
|---|---|---|---|---|
| | n | iN | F1 | Fc |
| | I | ii | F2 | Fb |
| | z | iy | F3 | F4 |
| | m | in | G1 | Ga |
| | @181; | Ii | G2 | Gb |
| | Z | Iy | G3 | Gc |
| | Z | iiy | G3 | Gd |
| | M | In | G1 | Ga |
| | M | im | G1 | Gb |
| | iM | Im | G2 | Gc |
| | @181;y | Iz | G3 | Gd |
Regularisation level 2 now consists in replacing the alternative STA codes with the standard ones, resulting in a further loss of distinction. In the STA definition tables, those codes that exist only in level-0 and level-1 STA, but no longer in level-2 STA, are highlighted in light red. Further simplifications to the representation of characters in the GC file are possible, leading to levels 3 and 4, but these may be left outside the scope of this page. Users may also define their own regularisations, not only to the GC file but to all files by further simplifying the list of STA codes, and thereby removing distinctions of some rare characters.
All transliteration files have been converted to STA, and links to the resulting files are provided below Table 12.
It must be stressed that the STA alphabet has not been designed in order to be the new alphabet that shall replace all other (native) alphabets. Use of these files is complicated by the fact that all characters are encoded as two bytes, which require dedicated tools. It may be assumed that most if not all existing user analysis tools expect single-byte encoding of Voynich MS characters. Also, most users will not be interested in processing a text in which several hundred different characters are recognised.
Instead, STA is primarily an intermediate representation, that has the main advantage that all existing translations can be represented using it. All processing of STA files can now be done for all files in an identical manner. A first processing step will typically be one of simplification, i.e. reduction of the alphabet to a smaller size. This can be done using bitrans or other user-developed tools. As an example, a bitrans table ("rules file") to convert STA to 'nearest equivalent basic Eva' (a significant simplification) is already available here. Users are encouraged to define their own transliteration alphabets, which can then be used by converting any existing transliteration to it (see Figure 3).
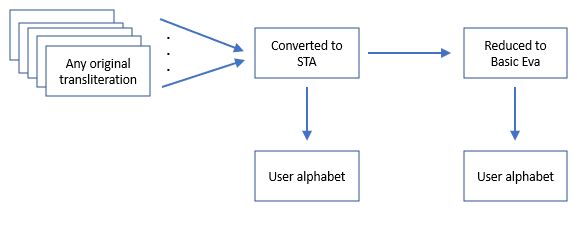
Figure 3: ways to set up a transliteration file in one's own alphabet
The following files were created from the latest files in IVTFF format (version 2.0). The only change that has been made during the conversion from the native alphabets to STA1 was to remove both full-line comments and inline comments.
Unlike in earlier versions, dedicated comments to indicate paragraph start and end, and text interruptions due to drawings, have been kept, and so have uncertain readings in [...] brackets.
| Origin | Code | Version | STA level 0 | STA level 1 |
|---|---|---|---|---|
| Currier / D'Imperio | CD | 2a | C-D STA level 0 | C-D STA level 1 |
| FSG | FG | 2a | FSG STA level 0 | Same as level 0 |
| Takahashi | IT | 2a | IT STA level 0 | Same as level 0 |
| voynichese.com | VT | 0e | VT STA level 0 | Same as level 0 |
| Zandbergen-Landini | ZL | 3b | ZL STA level 0 | Same as level 0 |
| G. Claston | GC | 2a | GC STA level 0 | GC STA level 1 |
| "Reference" | RF | 1b | RF STA level 0 | Same as level 0 |
Note: the IT, VT and GC files still include the incorrect label on f89v2, as locus f89v2.26 , but in the ZL and RF file this has been removed.
 |
 |
 |
 |