Voynich MS - Analysis - Word paradigms

Several authors have identified structures in the composition of words in the Voynich MS. These are, roughly in chronological order:

3.1.1 Tiltman's split in roots and suffixes (1)

Tiltman observed that many words in the stars or recipes section (which was the only sample that, initially, he had available for a detailed analysis) were composed of two parts. He set up the a table in Plate 17 of his publication, which is shown below:

Roots	Suffixes
ok of	an ain aiin aiiin
ot op	ar air aiir aiiir
qok qof	al ail aiil aiiil
qot qop	or
ch	ol
Sh	ey eey eeey
d	edy eedy eeedy
s

Every combination of a 'root' and a 'suffix' gives a valid word. He roughly subdivided the suffixes into three groups, depending on whether they contain a, o or e. Tiltman observes that the suffixes (which he also calls 'finals') are often found standing alone in the stars section of the MS.

Assuming that an empty root or an empty suffix would be allowed, this model can generate 272 different words. While this number is extremely low compared to the actual number of different words in the MS, the majority of frequent words are included in this list. The most frequent word not covered by it is the 19th ranked dy (2). In fact, several of the most frequent words that cannot be modeled are due to the missing single suffix y.

Regarding the second type of suffix, some of the combinations are so rare that I have been uncertain whether to take any account of them at all. Some are very common indeed. It seems to me that each of these combinations beginning with a has its own characteristic frequency which it maintains throughout the MS and independent of context (except in case where two or more a groups are together in series, as referred to later). These a groups, e.g. ar or aiin, frequently occur attached directly to "roots", particularly ok (of), ot (op), d and s. okaiin (ofaiin), qokaiin (qofaiin) and daiin rank high among the commonest words in the MS.
I am unable to avoid the conclusion that the occurrences of the symbol e up to three times in one form of suffix, and the symbol i up to three times in the other must have some systematic significance.

Tiltman also presents an observation, apparently offered to him by one Peter Long, "that the a groups might represent Roman numerals. Thus aiin might represent 'iij', and ar ar al 'xxv', but this, if true would only present one with a set of numbered categories, which doesn't solve the problem. In any case, though it accounts for the properties of the commoner combinations, it produces many impossible ones."

3.1.2 Mike Roe's generic word

The following pattern was contributed to the Voynich MS mailing list (3) by one of its original participants Micheal Roe. His system is represented here, both using the EVA alphabet and in Voynich characters. Each path represenst a valid word, and Mike suggested that this could perhaps present evidence of grammar of the Voynich language:

  
                      +- o  --+  +- r -+
 o   --+           +--+       +--+     +--+
       |  +- t -+  |  +- cho -+  +- l -+  |
 qo  --+--+     +--+                      |
       |  +- k -+  |  +- e ---+           |
 cho --+           |  |       |           |
                   |  +- ee --+           |
                   |  |       |           |
                   +--+- che -+-- y ------+------>
                   |  |       |           |
                   |  +- ch --+           |
                   |  |       |           |
                   |  +- sh --+           |
                   |  |       |           |
                   |  +-------+           |
                   |                      |
                   |  +- al ---+          |
                   |  |        |          |
                   +--+- am ---+----------+
                      |        |
                      +- ain --+
                      |        |
                      +- aiin -+

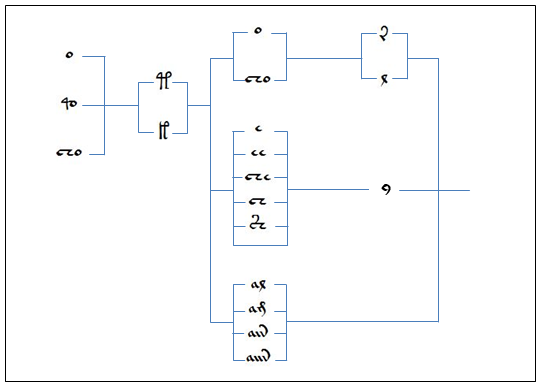
This model can generate only 120 different words, and was obviously not intended to represent all words in the MS. The most frequent word that cannot be modeled is the 12th ranked qokeey (see note 2).

3.1.3 Robert Firth's split into odd and even groups

Another early mailing list member, Robert Firth, based his analysis on the pages in the MS written in Currier's A language. Looking at all words (which he calls groups) that occur at least four times, he set up a list of 'odd letters' and a list of 'even letters', such that each group is composed of an odd letter followed by an even letter. This is explained in his Note Nr.24 (preserved local copy), which uses Currier's transliteration system (4).

The split is not entirely unambiguous, but according to Firth, the system works reasonably for the words he considered. The approach is similar to Tiltman's split, and is illustrated below. I have taken the liberty to rearrange the two columns and group similar items together, in order to improve the layout. This also makes it more easily comparable to Tiltman's system.

Odd letters	Even letters
s d	dy dal daiin
k t	al ar am
o ok ot	ain aiin oiin
qo qok qot	ey eey
yk yt	or ol eol
ch Sh Sho	chy chey
cKh cTh cPh	cho chol chor
chk cht	Shy
chcKh chcTh chcPh	y (?)

This model can generate 483 combinations. If we were to enforce that both columns must be represented, then this model would not be able to generate any unattached finals. Adding an empty slot to the first column increases the number of combinations to 504, but a number of these are no longer unique. Since this model was derived from the A language, it does not model any of the specifically B-language words, such as fourth-ranked chedy.

3.2 Jorge Stolfi's ground-breaking work

3.2.1 Split into 'soft' and 'hard' characters

Jorge Stolfi discovered a new structure in the words of the Voynich MS, by grouping all characters into 'soft' and 'hard' and showing that the vast majority of words consists of one, two or three groups, which he calls prefix, midfix and suffix. This was primarily based on text in Currier's B language. The prefix and suffix consist only of 'soft' characters, and the midfix only of 'hard' characters. Some time after this, Stolfi also defined a more complete (yet more complicated) description of the words (see 'word grammar' below). However, the simple principle behind the prefix-midfix-suffix structure makes it worthwhile to look at first.

It is explained in detail on a preserved local copy from his original web site. It may be summarised as follows:

The following characters are 'hard' characters and build the optional midfix (usually called stem) of a word:
t k Sh ch p f cTh cKh cPh cFh e .

All other characters are soft, and build the prefix and suffix:
q a o y d s j m n r l i .

Stolfi provides lists of the most frequent prefixes, midfixes, suffixes and unifixes, indicating that especially the soft-character groups go down in frequency very fast. This is demonstrated below in a partial screenshot of his page.

The most frequent word that cannot be modeled by this method is 112-th ranked aiiin. Undoubtedly, this is only due to the fact that he truncated his lists.

3.2.2 Fine structure

Later, Stolfi analysed a 'fine structure' of words in the Voynich MS. This is also known as the 'OKOKOKO' paradigm. It is also explained in detail in a preserved local copy from his web sote.

According to this model, strings of Voynich text (apparently ignoring spaces) may be parsed as:

He also calls the sequence "I X E" by the symbol "K", which explains the title of this paradigm. He lists the specific combinations that are allowed for K.

3.2.3 Word grammar

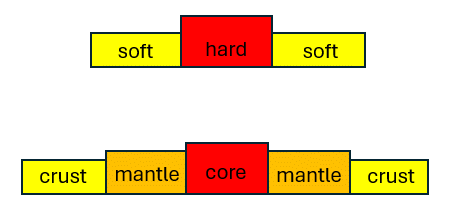
Most of the features found by Jorge Stolfi were later combined into what he calls the grammar of Voynich words. It is his most complete and most accurate breakdown of the word structure into a set of rules, and splits all characters into three groups which he calls core, mantle and crust. In addition, the three characters o a y, which he calls 'circles', play their own role in this system. It is explained in great detail on this page from his web site, while the formal grammar definition is here.

The relation between hard/soft and core/mantle/crust at the word level can be shown graphically, as follows, where each item can be empty:

	core	mantle	crust	circles
soft			d l r s n x i m g	o a y
hard	t k p f cTh cKh cPh cFh	ch Sh ee (e)

While the character e has its own additional rules, it best fits the mantle so I have included it there for simplicity.

3.3 Hidden Markov Modelling

This topic was already described on a previous page, where some of its results reflected on the word structure.

3.4 Slot alphabets

3.4.1 Introduction

Several authors have independently arrived at the idea that the words of the Voynich MS could be generated by picking subsets of characters from slots. This is best described by the examples that are given below.

3.4.2 First example

The first example that I am aware of is included in a series of posts in the Ninja Forum (see note 3) by a contributor writing under the name (or pseudonym) ThomasCoon. Starting on 30 October 2016 he posted two slightly different versions. Below, I copy the first, with only editorial changes:

Words can be constructed by picking items from some of the columns, always from left to right. As an example of its application, the word choteol can be constructed by picking items from columns 2, 3, 4, 6, 7 and 8 (in that order).

0	1	2	3	4	5	6	7	8	9	10	11
q d	s ch sh	o e y ol	k t p f	ch sh	e ee eee	o a	r l	d s ch	a o	n m in r iin l	y

0	1	2	3	4	5	6	7	8	9	10	11
q d	s ch sh	o a y ol	k t p f	ch sh	e ee eee	o a y	r l	d s ch t?	o a	n m in r iin l	y s

The most frequent word that cannot be modeled by this system is one that includes a pedestalled gallows, namely 44th-ranked chcKhy.

It is of interest to compare this system with Stolfi's prefix-midfix-suffix paradigm. Using the second grid, let us see which slots have soft or hard characters.

3.4.3 More general considerations

	0	1	2	3	4	5	6	7	8	9	10	11
soft	q d	s	o a y ol				o a y	r l	d s	o a	n m in r iin l	y s
hard		ch sh		k t p f	ch sh	e ee eee			ch t?

In 2021 I wrote a paper in which I demonstrated that the method proposed by Gordon Rugg, in which he proposed that the MS was created as a fake by moving grids over a large table of word fragments, can be generalised into a slot alphabet. In this case, each slot does not necessarily include single characters, but can also have character combinations. The interested reader may find this paper on-line (6).

3.4.4 Massimiliano Zattera's slot alphabet

The most recent and well-documented example was presented at the 2022 Voynich MS Conference organised by the University of Malta. Both the paper and the presentation by Massimiliano Zattera are available online (7). His slot alphabet is included below, again with only editorial changes.

0	1	2	3	4	5	6	7	8	9	10	11
q s d	o y	l r	t k p f	ch sh	cth ckh cph cfh	e ee eee	s d	o a	i ii iii	d l r m n	y

In his publication he analyses the quality of this model in significant detail, and he also compares it with other models. The most frequent word that cannot be modeled by it is 89-th ranked cheky.

Also here, we can analyse how the slots are distributed over soft and hard characters.

In this case, we see that the slot alphabet is perfectly compatible with Stolfi's prefix, midfix and suffix approach. In his paper, Zattera also shows the accordance of his slot system with Stolfi's grammar expressed as core/mantle/crust:

3.4.5 Brief summary of these examples

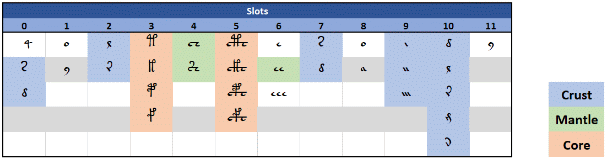
Whether it is just a coincidence or not, all three cases of single-character slot tables discussed above use 12 slots. It should be noted that the second case does not give any concrete example, and perhaps the number 12 is just an obvious choice.

The systems of ThomasCoon lack the pedestalled gallows, which was also the case for the systems of Tiltman and Roe. Firth's system includes them and so does Zattera.

Both specific examples (ThomasCoon and Zattera) have in common that certain Voynich characters appear in more than one slot. This is probably unavoidable, and it means that some short words can be generated in more than one way.

I consider that this last point could perhaps be avoided by having fewer slots, and allowing a cycle back between two specific points. This will be elaborated further in a future update of this page.

	0	1	2	3	4	5	6	7	8	9	10	11
soft	q s d	o y	l r					s d	o a	i ii iii	d l r m n	y
hard				t k p f	ch sh	cth ckh cph cfh	e ee eee

3.5 Word paradigms, summary

The results presented in this page are critally important for anyone interested in translating the text of the Voynich MS. The fact that structures like the ones introduced in this page exist, tells us that the MS text is not one that was encrypted from an Indo-European plain text using the type of encryption available in the early 15th Century. Any tentative solution working along these lines will necessarily fail.

The exact word structure has not been identified definitely. This page shows several cases, and in general one may observe that the simple paradigms will 'cover' or 'explain' a smaller percentage of the word types in the MS, while the more complicated ones cover a larger percentage.

The word structure is also likely to completely explain the anomalously low entropy values of the Voynich MS text, though what is cause and what is effect is not yet fully understood.

Analysis Section ( 3/5 ) - Word structure

3.1 Introduction